
AI-机器学习-第一课
AI-机器学习-第一课
学习准备
本人使用的是MacBook进行课程的学习, 需要安装jupyter notebook.
安装参考文档: https://zhuanlan.zhihu.com/p/33105153
需要注意的是由于安装的包没有包含ipympl的py库, 因此matplotlib动态交互加载不了, 安装命令:
pip install ipympl
运行jupyter notebook命令:
jupyter notebook
课程需要的一些资料链接, 原链接是GitHub的, 对国内不太友好, 所以使用的是码云的:
原GitHub地址: https://github.com/kaieye/2022-Machine-Learning-Specialization
可以使用码云同步下仓库.
什么是机器学习?
Arthur Samuel(编写了第一个自学习的跳棋程序)给出的定义:
Field of study that gives computers the ability to learn without being explicitly(明确地) programmed.
一般来说, 给学习算法的机会越多, 它的表现越好.
机器学习算法简介
学习算法的建议: 高效地使用工具进行有效的学习.
Supervised Learning 监督学习
目前使用最多, 发展最迅速的算法.
常见的监督学习是指学习x到y或输入到输出映射的算法.
关键特征是提供学习算法示例以供学习, 这包括正确答案, 给定输入x的正确标签y, 并且通过查看正确的输入x和所需输出标签y对, 学习算法最终学会只接受输入而不需要输出标签并给出合理准确的预测或猜测.
一些监督学习的例子:
| Input(X) | Output(Y) | Application |
|---|---|---|
| spam?(0/1) | spam filtering | |
| audio | text transcripts | speech recognition |
| English | Spanish | machine translation |
| ad, user info | click?(0/1) | online advertising |
| image, radar info | position of other cars | self-driving car |
| image of phone | defect?(0/1) | visual inspection |
在上面所有应用中, 首先使用输入示例x和正确答案(标签y)来训练模型, 模型学习后, 模型可以采用全新的输入x, 并尝试适当的对应输出y.
Regression(回归): 从无限多个可能的数字中预测数字.
Classification(分类): 预测类别(category), 输出的类别是有限可能的集合. 给这些类别划分出边界的函数曲线.
Supervised Learning
Learns from being given "right answers"
# 回归
Regression
Predict a number
infinitely many possible outputs
# 分类
Classification
predict categories
small number of possible outputs
UnSupervised Learning 无监督学习
在数据中找到一些结构和模式, 或找到一些有趣的东西.
Clustering(聚类): 获取没有标签的数据并尝试自动把它们分组到集群中. 典型例子是谷歌的新闻搜索.
Anomaly detection(异常检测): 用于检测异常事件.
Dimensionality reduction(降维): 可将一个大数据集压缩成一个小得多的数据, 同时丢失尽可能少的信息.
Unsupervised Learning
Data only comes with inputs x, but not output lables y.
Algorithm has to find "structure" in the data.
# 聚类
Clustering
Group similar data points together.
# 异常检测
Anomaly detection
Find unusual data points.
# 降维
Dimensionality reduction
Compress data using fewer numbers.
随堂小测验(Quiz):
Of the following examples, which would you address using an unsupervised learning algorithm?
- Given email labeled as spam/not spam, learn a spam filter.
- Given a set of news articles found on the web, group them into sets of articles about the same story.
- Given a database of customer data, automatically discover market segments and group customers into different market segments.
- Given a dataset of patients diagnosed as either having diabetes or not, learn to classify new patients as having diabetes or not
正确答案: 2和3是无监督学习. 1和4是监督学习的分类.
Reinforcement Learning 增强学习
暂时没有讲授.
代码
# hello, world
print("hello, world!")
# print statements
variable = "right in the strings!"
print(f"f strings allow you to embed variables {variable}")
线性回归模型
Linear Regression Model
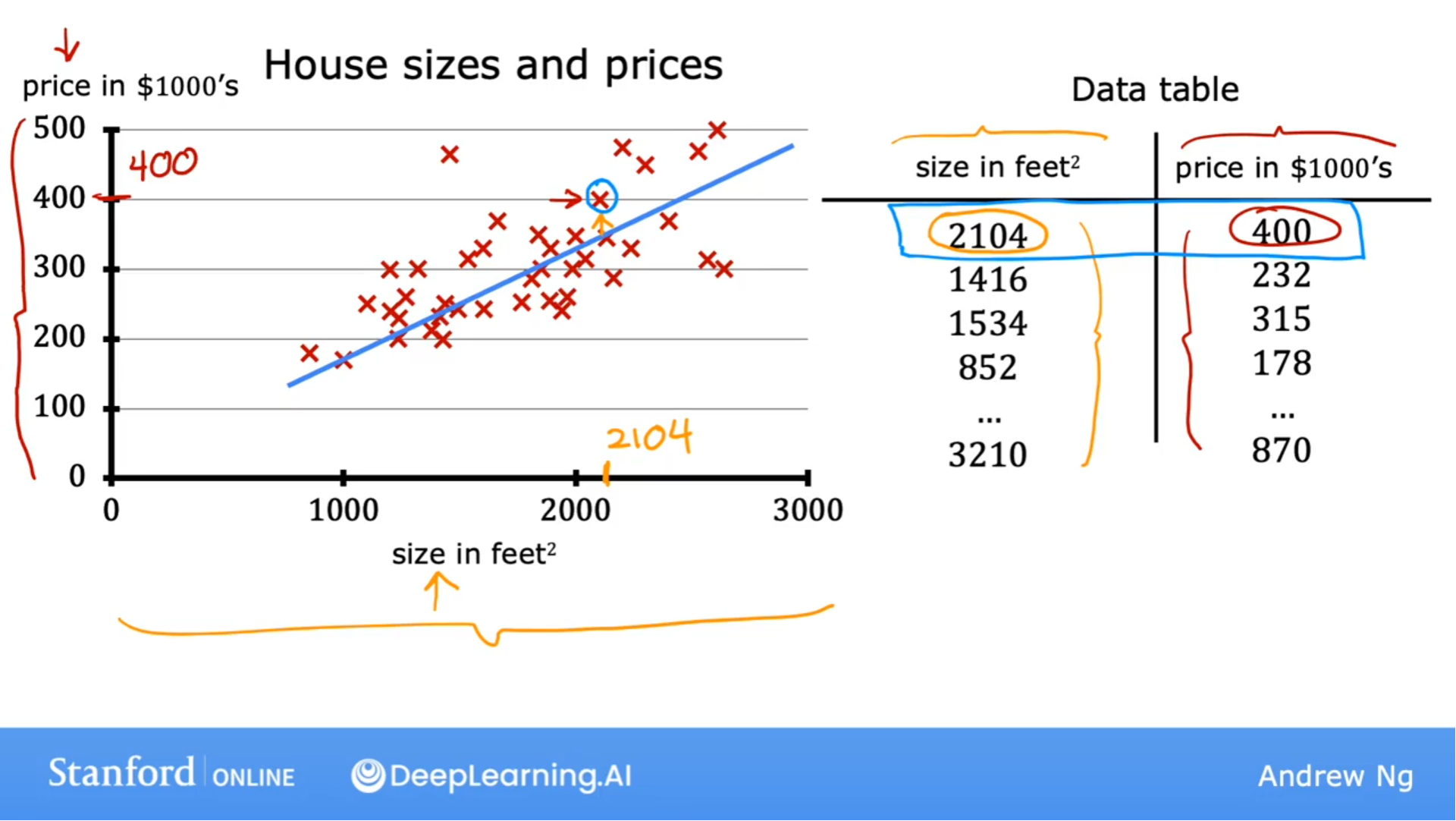
常用术语

训练集(Training Set): Data used to train the model.
x: 输入参数(input variable), 特征(feature)
y: 输出变量(output variable), 目标变量(target variable)
m: 训练集中数据的数量
(x, y): 表示单个训练数据
($x^{(i)}$, $y^{(i)}$): 表示制定的具体的单个训练数据, 其中i表示数据的访问下标, 表格数据是从1开始, 而python中是从0开始.
监督学习算法流程
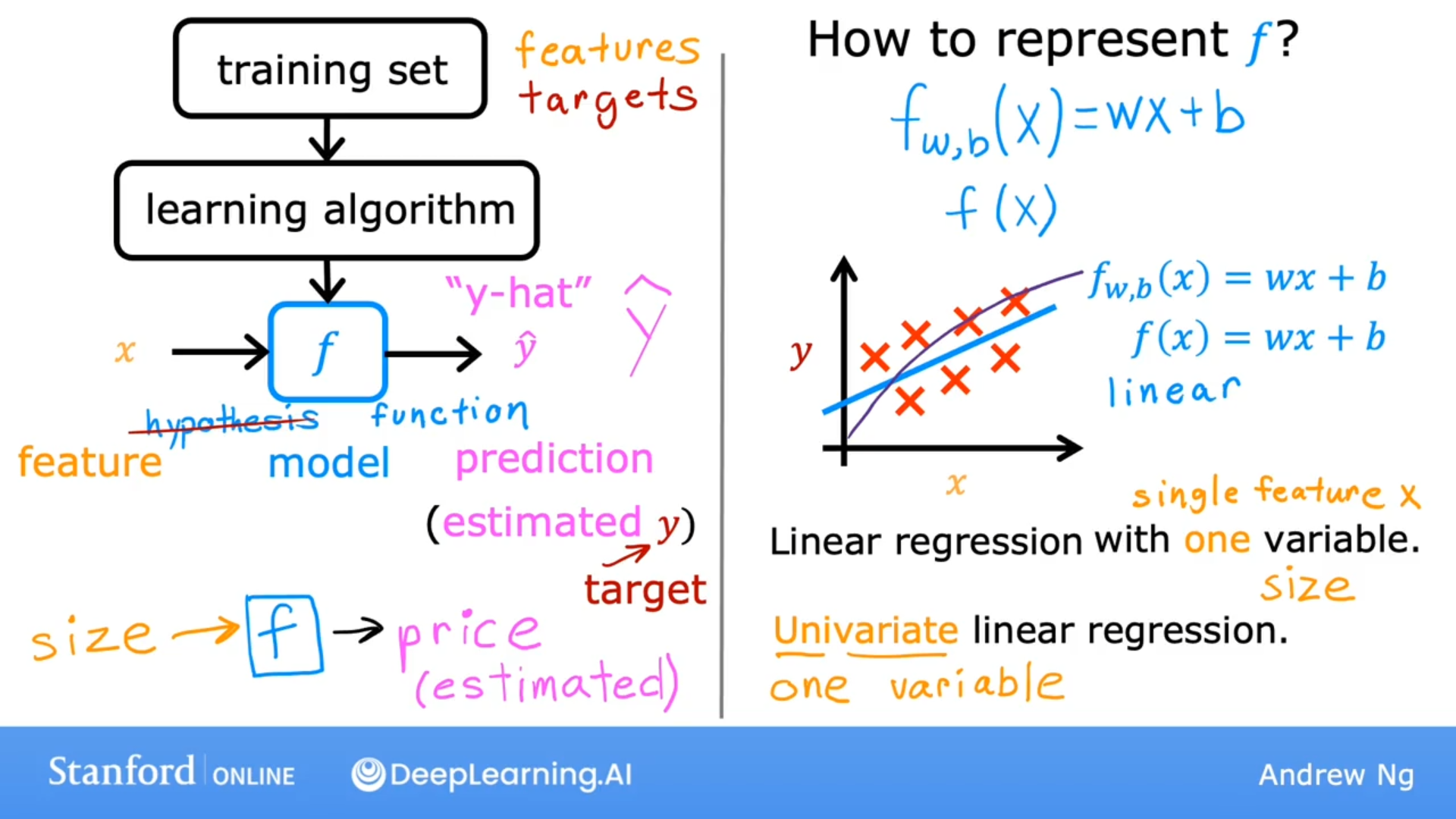
y-hat是对输出结果的预测值.
常用f下角标来表示模型的参数列表.
上面图片中的函数f是只有一个特征变量x, 成为单变量线性回归(Univariate linear regression)
线性函数f: $f_{w,b}(x^{(i)}) = wx^{(i)}+b$
代码
机器学习经常使用的库:
- NumPy, 用于科学计算
- Matplotlib, 流行的展示数据的库
# 导入NumPy和matplotlib.pyplot
import numpy as np
import matplotlib.pyplot as plt
# matplotlib.pyplot使用样式表
plt.style.use('./deeplearning.mplstyle')
# 使用numpy, x数据集的下标和y数据集的下标一一对应
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
# 访问训练集中数据的数量
# x_train.shape中保存的是一个数组中的数据个数
# 如果有多个特征变量, 则x_train则会有多个数组
m = x_train.shape[0]
# 下面的方法也能获取到训练集的数据数量
m = len(x_train)
# 访问训练集中的单个数据
i = 0 # python从0开始,i=0访问的是第一个数据
x_i = x_train[i]
y_i = y_train[i]
# 展示数据图表
plt.scatter(x_train, y_train, marker='x', c='r')
# 图表标题
plt.title("Housing Prices")
# y轴的别名
plt.ylabel('Price (in 1000s of dollars)')
# x轴的别名
plt.xlabel('Size (1000 sqft)')
plt.show()
# np.zero(n)返回一个一维的NumPy数组,其中包含n个实体
# 实现简单的计算函数f的功能
def compute_model_output(x, w, b):
"""
f = w*x + b
三个双引号是python的模版字符串
参数:
x: m个数据数量的训练集,是个NumPy数组
w,b: 模型的参数
返回值:
f_wb: 函数值f的NumPy数组
"""
m = x.shape[0]
f_wb = np.zeros(m)
for i in range(m):
f_wb[i] = w * x[i] + b
return f_wb
成本函数
Cost Function

预测函数: $f_{w,b}(x^{(i)}) = wx^{(i)}+b$
y-hat值是通过函数f做出的预测值, 为了找到相应的w, b, 且衡量与训练数据的拟合程度, 于是有了成本函数:
$$J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{1}$$
其中$$f_{w,b}(x^{(i)})$$是y-hat的值
这个函数称为: 误差平方成本函数(Squared error cost function)
其中的1/2m是为了以后计算梯度下降值而使用的, 平方求导能消去1/2.
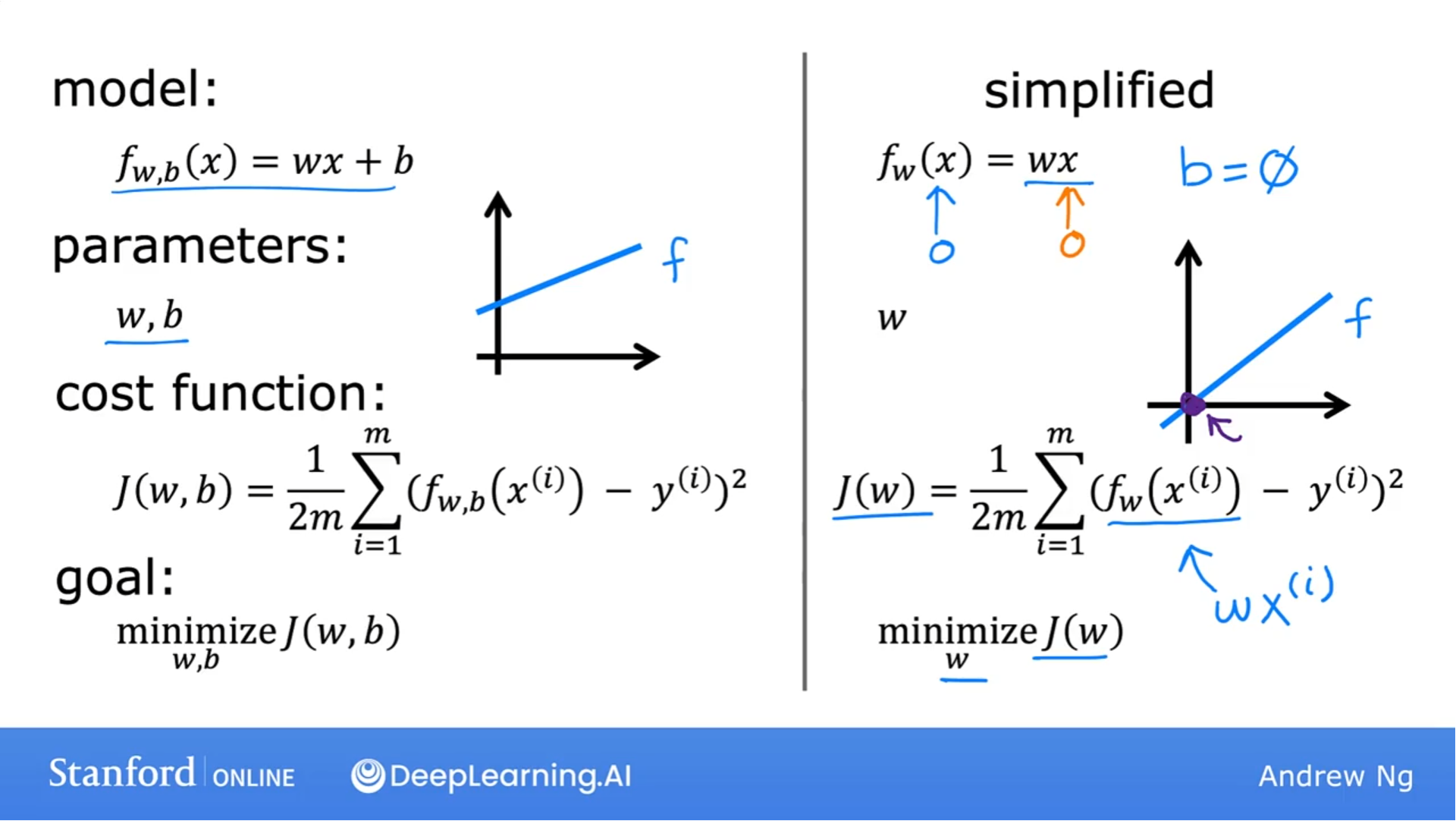
目标是追求最小化函数: $$J(w,b)$$, 右图是函数f的简化版.
函数f和成本函数J之间的直观对照:

线性回归的目标是找到参数w和b, 使得成本函数J的值最小.
更直观的函数对照图, 通过函数J与参数w, b形成的3D碗形曲面图, 还有成本函数J与参数w, b形成的同心椭圆(等高线图):
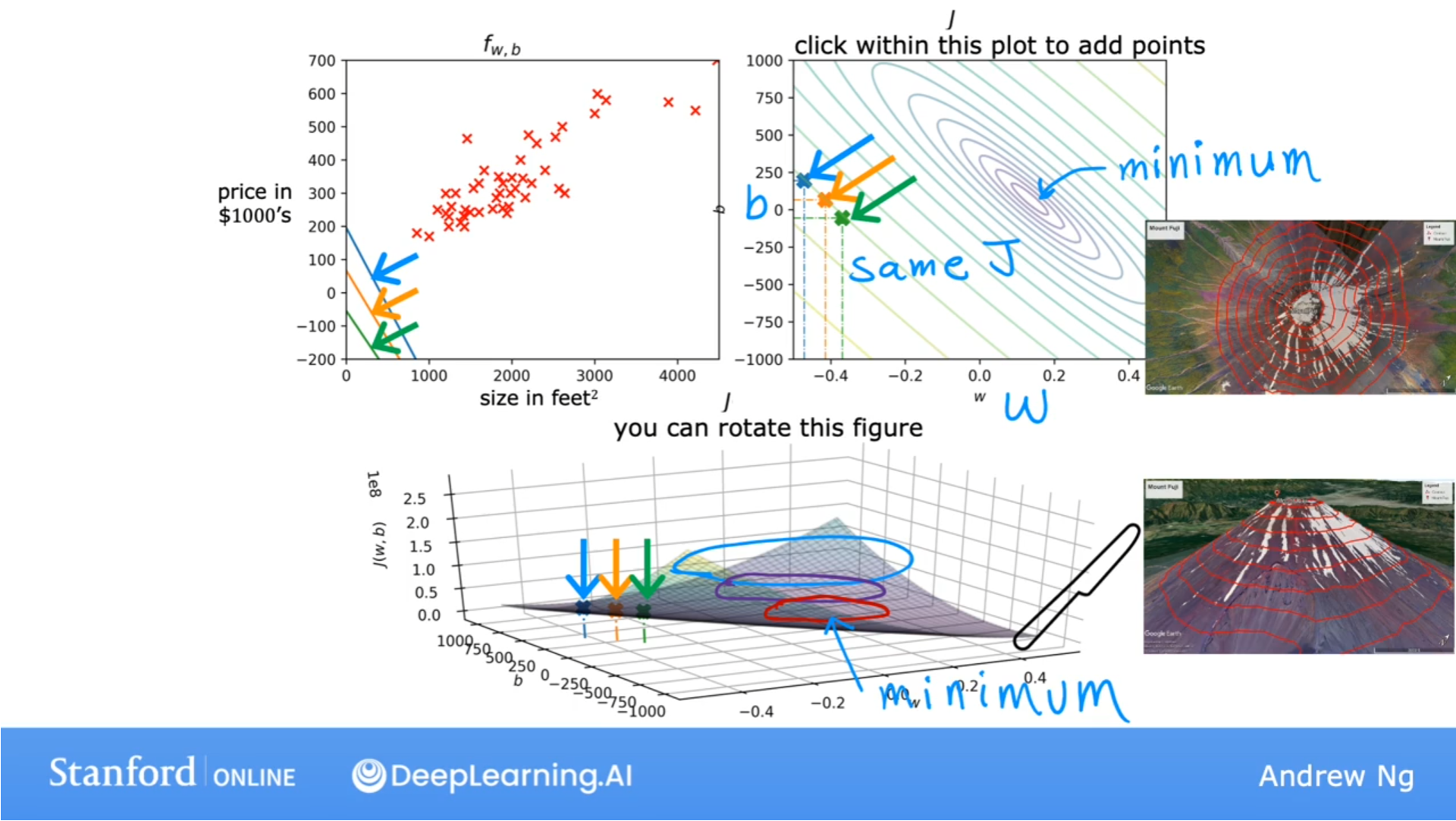
代码
# 导入库
import numpy as np
# 可以让用户在图表上进行拖动和修改的库
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclick, soup_bowl
plt.style.use('./deeplearning.mplstyle')
# 训练集
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
对于python版本的成本函数J, 因下标是从0开始, 所以i是从0到m-1:
$$J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{1}$$
其中函数f:
$$f_{w,b}(x^{(i)}) = wx^{(i)} + b \tag{2}$$
# 计算成本函数
def compute_cost(x, y, w, b):
"""
参数:
x: 训练集, NumPy数组
y: 目标值, NumPy数组
w,b: 模型参数
返回值:
total_cost: 成本函数的值, NumPy数组
"""
# 数据数量
m = x.shape[0]
# 记录成本函数平方合
cost_sum = 0
# range(m) 范围[0, m), 左闭右开
for i in range(m):
# 计算函数f的值, 即y-hat
f_wb = w * x[i] + b
# 计算预测值与实际值的差的平方
cost = (f_wb - y[i]) 2
# 汇总到cost_sum
cost_sum = cost_sum + cost
# 计算成本函数J的值, 注意缩进, 已经不在for循环里了
total_cost = (1 / (2 * m)) * cost_sum
# 返回成本函数J的值
return total_cost
梯度下降
概念
Gradient descent
梯度下降是一种可用于尝试最小化任何函数的算法, 而不仅仅是线性回归的成本函数.
梯度下降适用于更一般的函数, 包括适用于具有两个以上参数的模型的其他成本函数.
$$J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{1}$$
线性回归中, 参数的初始值是多少并不重要, 一个常见的选择是将它们都设置为0. 如将w, b设置为0.
使用梯度下降算法, 每次都稍微改变参数w和b以尝试降低成本函数J, 直到希望成本函数J稳定在或接近最小值. 需要注意的是, 对于某些成本函数, 可能存在不止一个可能的最小值.
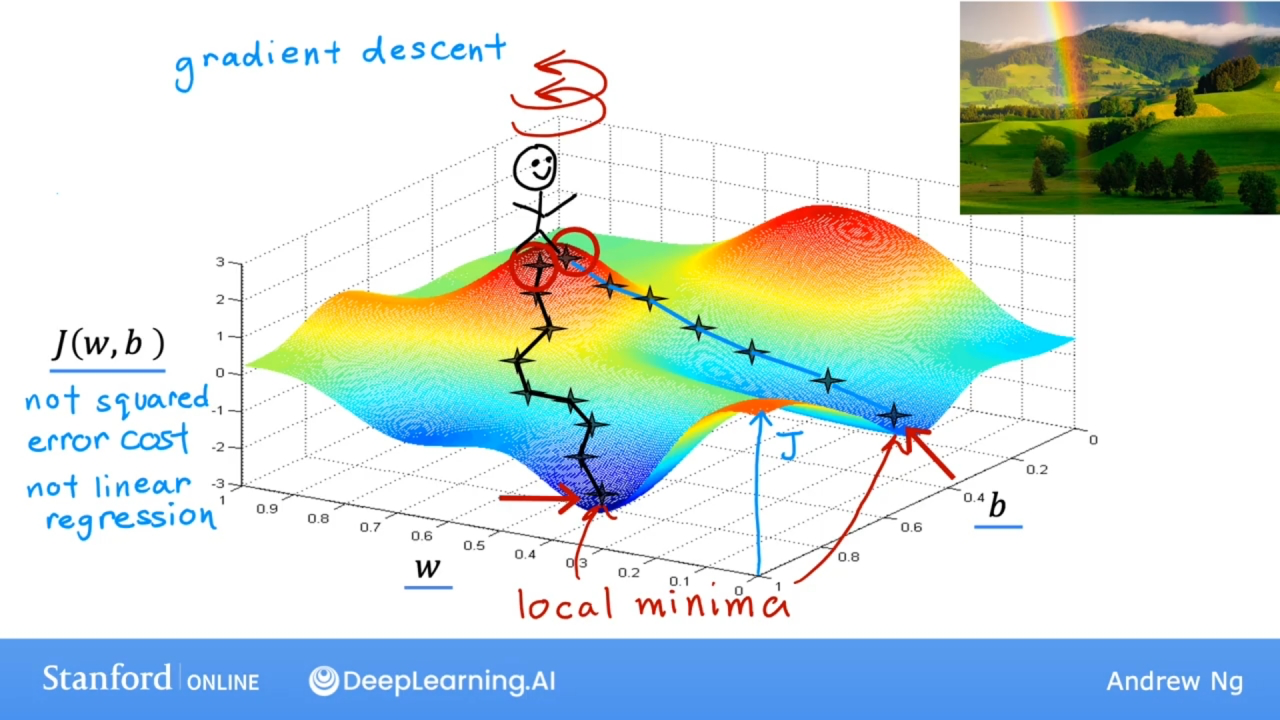
梯度下降就像在山顶寻找最快速到达山底的路径一样. 环绕四周, 找到最陡下降方向, 然后沿着这个方向下山; 走过一段路后, 再次重复找到最陡下降方向的过程, 然后到达山底.
由于选定的初始参数值(w和b)的不同, 有可能会到达另一个山底, 每个山底都是一个局部最小值(local minima).
公式

其中的$\alpha$表示学习率(Learning rate), 用来控制梯度下降的幅度, 始终是个正数.
$$w = w - \alpha \frac{\partial J(w,b)}{\partial w} $$中的$$\frac{\partial J(w,b)}{\partial w}$$是成本函数J对参数w的导数(Derivative)
$$b = b - \alpha \frac{\partial J(w,b)}{\partial b} $$中的$$\frac{\partial J(w,b)}{\partial b}$$是成本函数J对参数b的导数(Derivative)
上面的两个导数决定了下降的步数大小.
梯度下降算法, 就是重复参数w和b通过上述公式的计算过程, 直到算法收敛. 通过收敛成本函数J到达局部最小值.
在重复更新参数w和b时, 必须同时更新w和b, 缺一不可, 需按照下面步骤更新:
- $$tmpw = w - \alpha \frac{\partial J(w,b)}{\partial w} $$
- $$tmpb = b - \alpha \frac{\partial J(w,b)}{\partial b} $$
- $$w = tmpw$$
- $$b = tmpb$$
如果错误的将步骤3提前到了步骤2, 则会造成参数w和b不是同时(Simultaneous)更新.
原理
简化成本函数J只有一个参数w, 通过下面的图片, 公式到底做了什么:
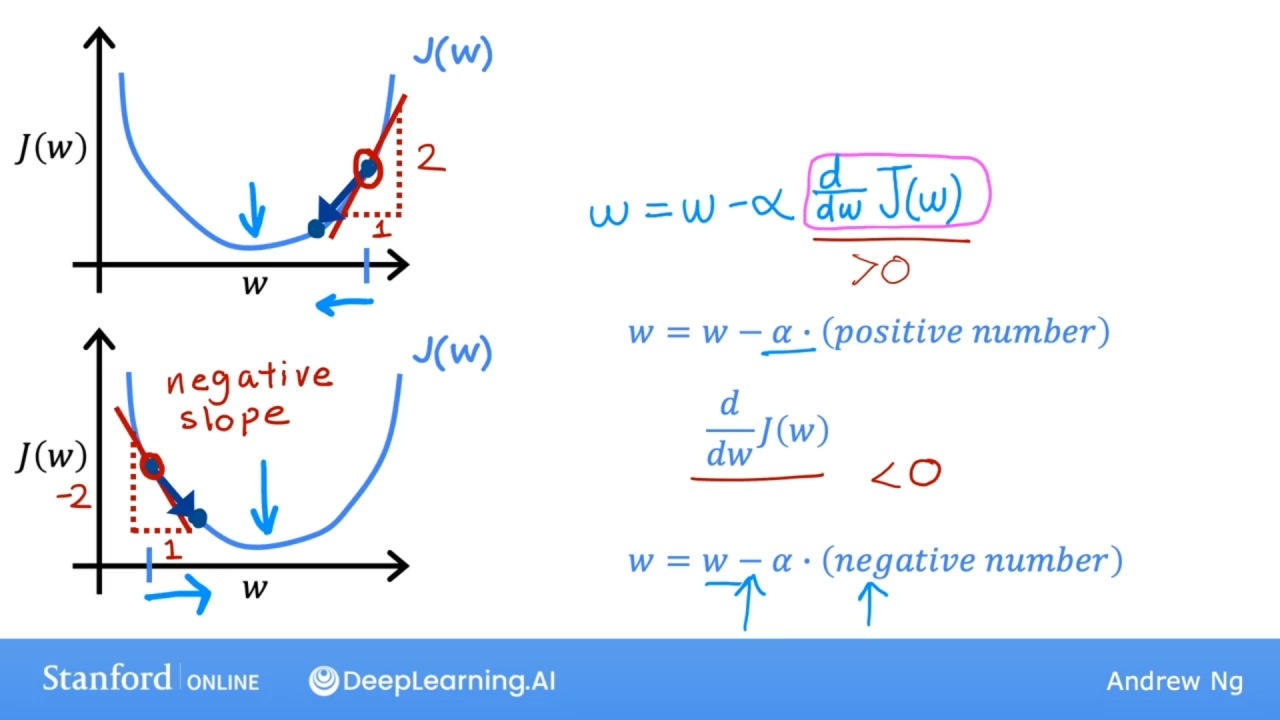
$$\frac{\partial J(w)}{\partial w}$$相当于成本函数J在w点上的切线的斜率.
当w取值在上面的点时, 此时斜率是一个正数, 而$\alpha$始终是个正数, 如图更新w值, w值减少, w值向让成本函数J取最小值的方向靠拢.
当w取值在下面的点时, 此时斜率是一个负数, 而$\alpha$始终是个正数, 如图更新w值, w值增加, w值也向让成本函数J取最小值的方向靠拢.
学习率
学习率太大或太小的情况:
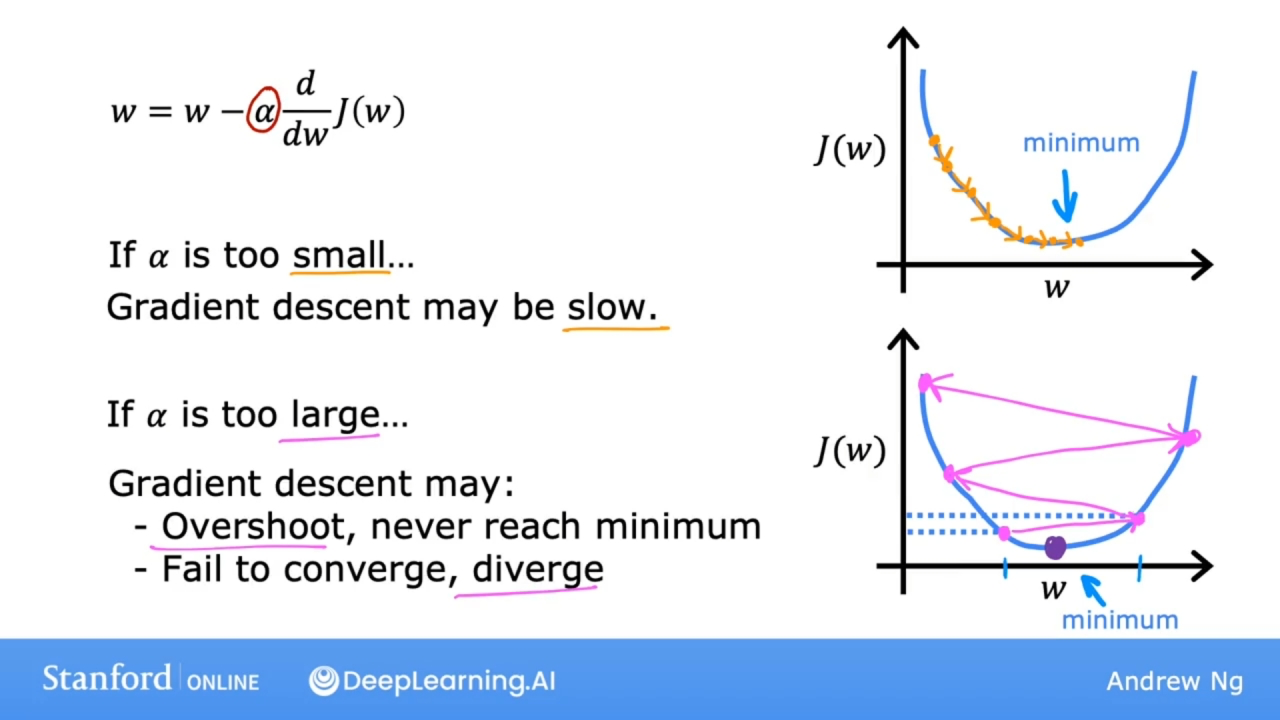
如果学习率$\alpha$太小, 则梯度下降的太慢了, 需要很多步骤才能到达最低限度.
如果学习率$\alpha$太大, 会造成:
- 梯度下降可能会过冲(Overshoot), 并且可能永远不会达到最小值.
- 大相交(Intersect)可能无法收敛, 甚至可能发散.
如果成本函数J有两个局部最小值:
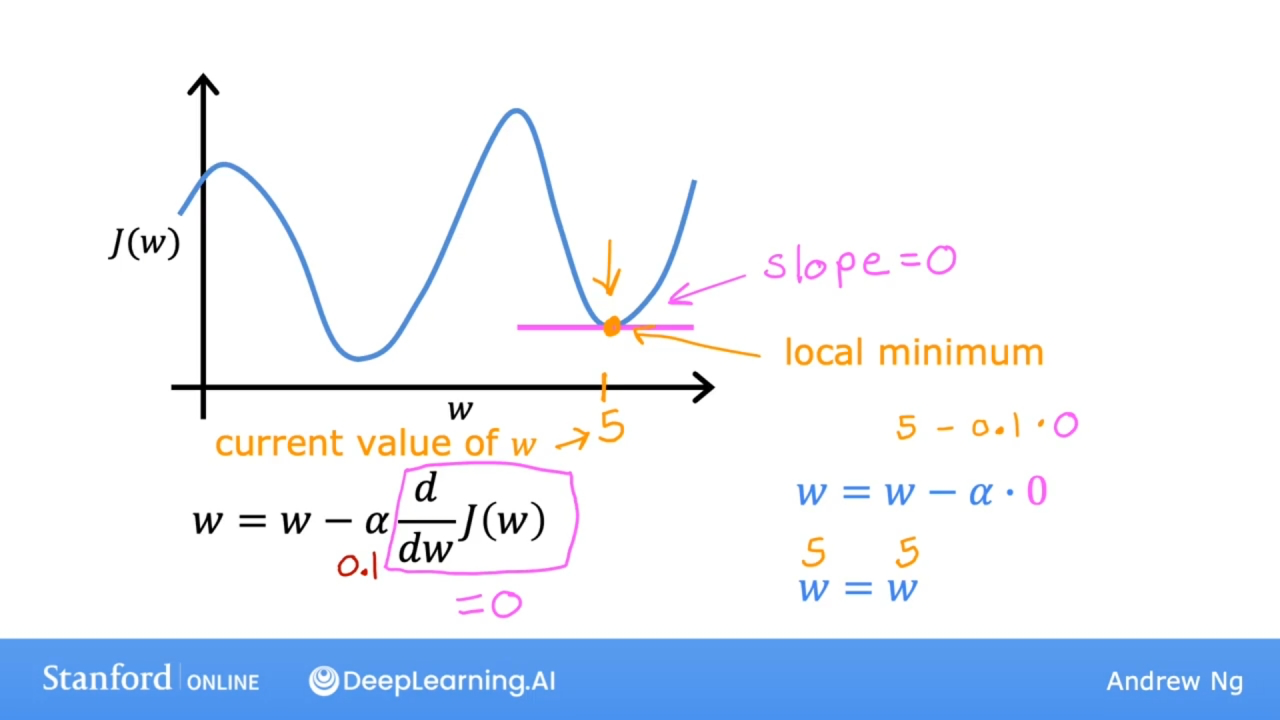
如果已经处于局部最小值, 则梯度下降将会使参数w保持不变, 因为局部最小值这个点的斜率为0.
使用固定的学习率$\alpha$同样能够达到局部最小值:
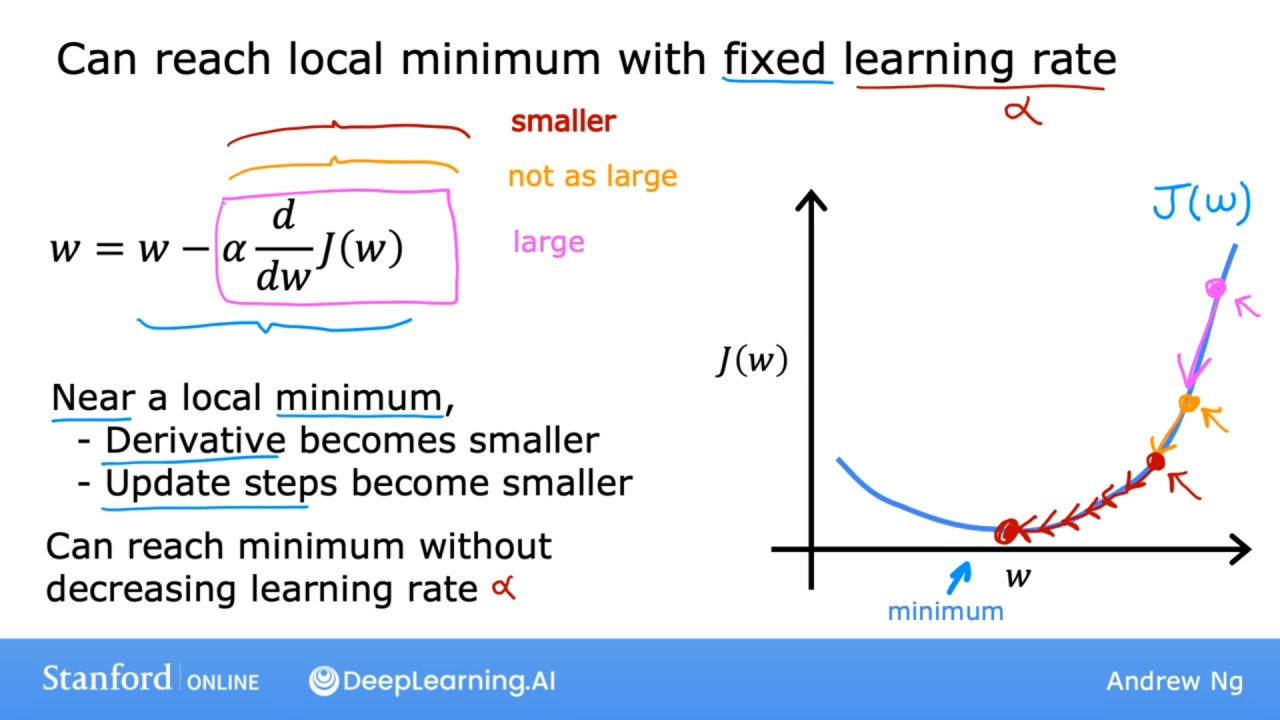
使用固定的学习率$\alpha$情况下, 导数的值会随着w值的下降, 因切线的斜率变小, 因而逐渐减少, 随后越来越小, 越接近局部最小值, 导数变得越小, 更新w值的步伐也越来越小.
实现
线性回归模型: $$f_{w,b}(x) = wx + b \tag{2}$$
成本函数: $$J(w,b) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{1}$$
梯度下降算法:
$$\begin{align*} \text{repeat}&\text{ until convergence:} ; \lbrace \newline ; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} ; \newline b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace \end{align*}$$
其中: $$ \begin{align} \frac{\partial J(w,b)}{\partial w} &= \frac{1}{m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \tag{4}\ \frac{\partial J(w,b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)}) \tag{5}\ \end{align} $$ 公式4, 5的推导过程:

成本函数J是一个凸函数(convex function, 函数的切线总位于函数曲线的下方, 或函数的二次导数大于0), 在凸函数上实现梯度下降时, 一个很好的特性是只要选择适当的学习率, 它总是会收敛到全局最小值.
函数运行过程图示
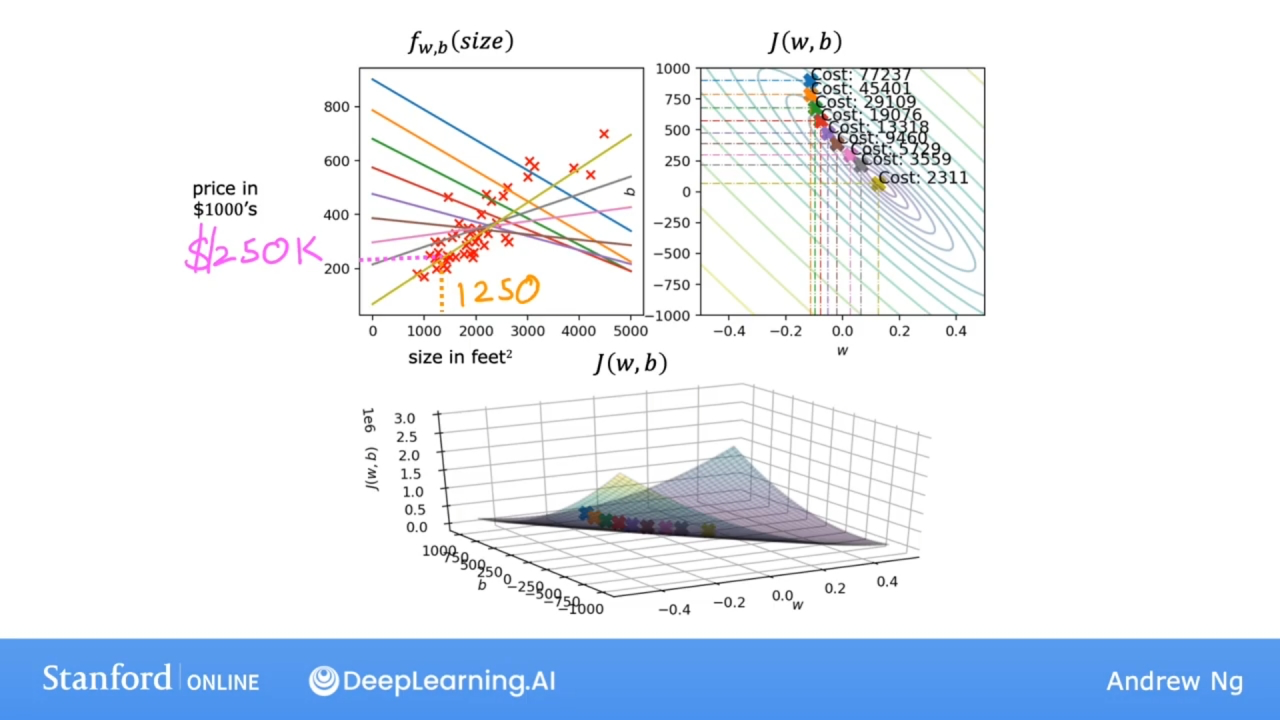
批量梯度下降
Batch gradient descent
在梯度下降的每一步中, 都使用所有的训练集, 而不仅仅是训练数据的一个子集.
在计算 $$\sum\limits_{i = 1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2$$时, 批量梯度下降都使用整个训练集.
还有其他的梯度下降算法, 不会查看整个训练集, 而是在每个更新步骤查看训练数据的较小子集.
代码
成本函数计算:
$$J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{1}$$
def compute_cost(x, y, w, b):
m = x.shape[0]
cost = 0
for i in range(m):
f_wb = w * x[i] + b
cost = cost + (f_wb - y[i])2
total_cost = 1 / (2 * m) * cost
return total_cost;
计算梯度, 即导数部分的计算: $$ \begin{align} \frac{\partial J(w,b)}{\partial w} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \ \frac{\partial J(w,b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \ \end{align} $$
def compute_gradient(x, y, w, b):
m = x.shape[0]
dj_wb = 0
dj_db = 0
for i range(m):
f_wb = w * x[i] + b
dj_wb_i = (f_wb - y[i]) * x[i]
dj_db_i = f_wb - y[i]
dj_wb += dj_wb_i
dj_db += dj_db_i
dj_wb = dj_wb / m
dj_db = dj_db / m
return dj_wb, dj_db
计算参数w和b梯度下降:
$$\begin{align*} \text{repeat}&\text{ until convergence:} ; \lbrace \newline ; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} ; \newline b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace \end{align*}$$
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function):
"""
参数w_in, b_in是初始的w, b的值
参数alpha, 是学习率
参数num_iters, 是循环迭代次数
"""
# 把参数w的初始值w_in深拷贝一份给w, 避免更新全局变量w_in
w = copy.deepcopy(w_in)
# 记录每次迭代的成本函数J的值和参数w, b的值
J_history = []
p_history = []
b = b_in
w = w_in
# 循环次数num_iters
for i in range(num_iters):
# 计算每次梯度下降的值
dj_dw, dj_db = gradient_function(x, y, w, b)
# 更新参数w和b
w = w - alpha * dj_dw
b = b - alpha * dj_db
# 次数小于10万时候,记录成本函数J和参数w, b的值
if i < 100000:
J_history.append(cost_function(x, y, w, b))
p_history.append([w, b])
# 打印10次循环的成本函数J和参数w, b的值
if i % math.ceil(num_iters/10) == 0:
print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",
f"w: {w: 0.3e}, b:{b: 0.5e}")
return w, b, J_history, p_history
调用梯度下降函数
# 初始化参数w和b的值
w_init = 0
b_init = 0
# 循环迭代次数和学习率
iterations = 10000
tmp_alpha = 1.0e-2
# 调用梯度下降函数
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, iterations, compute_cost, compute_gradient)
# 打印返回的结果
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")
多维特征与矢量化
多元线性回归
比如预测房价, 不知有尺寸信息, 还有其他, 如下面的表格
| 尺寸 | 房间数量 | 楼层 | 房屋年龄 | 房价 |
|---|---|---|---|---|
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | |
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
上面的数据则有$x_1$, $x_2$, $x_3$, $x_4$这四个特征.
使用$x_j$表示第j个特征(feature)
使用n表示特征的数量
使用$x^{(i)}$(x带箭头)表示第i个训练数据
使用$x^{(i)}_j$(x带箭头)表示第i个训练数据的第j个特征
则模型函数f则表示为:
$$f_{w,b}(x) = w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + b \tag{2}$$
一般来说, 如果有n个特征, 可表示为:

可使用矢量化的参数w和x来简化表示模型函数.
其中矢量w表示模型参数集, 矢量x表示特征参数集.
矢量w和矢量x的乘积称为点积(dot product), 其等价于矢量w和矢量x相同下标的参数值的乘积和, 如上图所示.
上面使用的多个特征模型称为多特征线性回归(multiple linear regression), 也称为多元线性回归.
矢量化
使用矢量化既可以缩短代码, 又可以提高运行效率, 能充分利用GPU的并行处理能力, 更快地执行代码. 如下图:

推荐使用NumPy库进行矢量乘积运算.
矢量化能提高运行效率的原理解释:
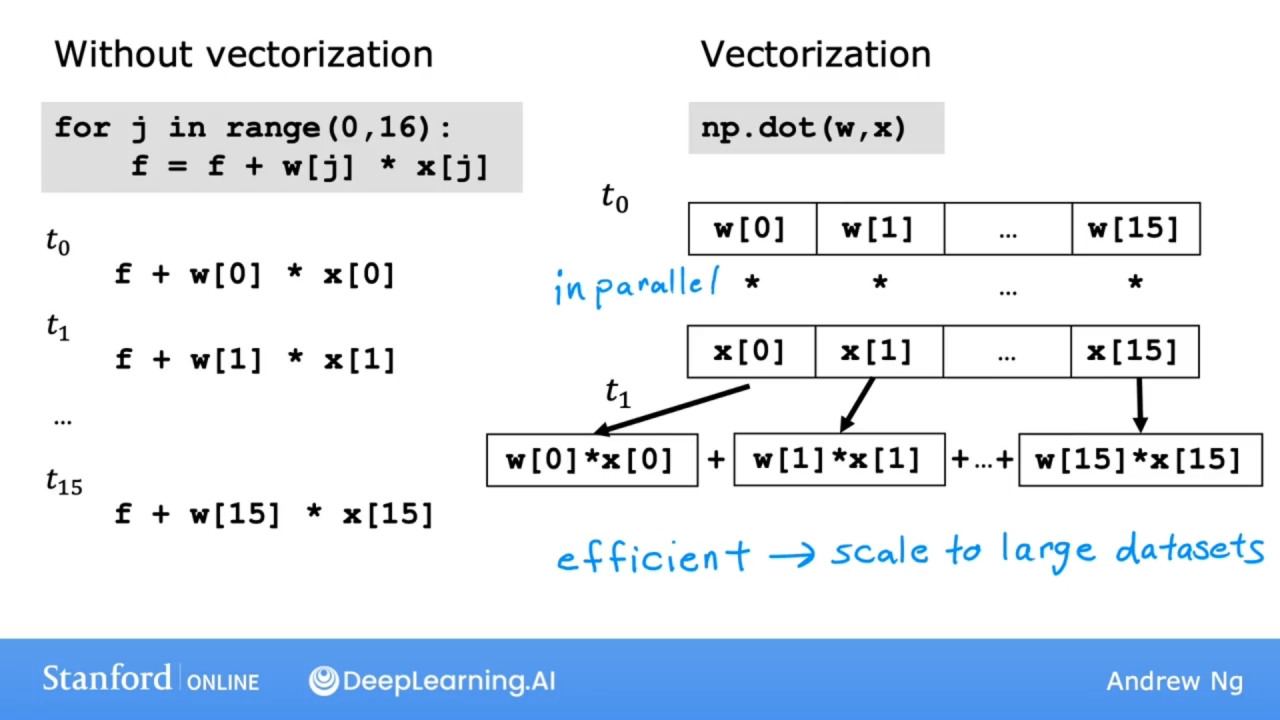
可以看到不使用向量化, 每次的运算都是一步步进行的, 是串行的.
而使用向量化, 则每次都能并行多个运算, 是并行的.
矢量化能提高线性回归运算速度原理:

使用NumPy的数组(矢量化).
代码
练习使用NumPy库.
NumPy文档官网: https://numpy.org/doc/stable/
# 导入库
import numpy as np
# 用于显示时间的库
import time
# 创建全是0的一维数组, 数组里的元素都是float64类型
a = np.zeros(4)
a = np.zeros((4,))
# 创建全是0到1的随机数的数组, 数组里的元素都是float64类型
a = np.random.random_sample(4)
# 创建从0到3的一维数组, 数组里的元素都是float64类型
# 如果不写4后面的. 则数组里的元素是int64类型
a = np.arange(4.)
# 创建包含4个随机数的一维数组, 数组里的元素都是float64类型
a = np.random.rand(4)
# 将普通的python数组包装成NumPy的数组
# 下面包装后的数组元素全部为int64整型
a = np.array([5,4,3,2])
# 如果其中有一个(5.)是float64类型,则数组元素都变为float64类型
a = np.array([5.,4,3,2])
# 创建新数组,为[0 1 2 3 4 5 6 7 8 9]
a = np.arange(10)
print(a)
# 使用下标访问数组元素,下标从0开始
print(f"a[2] = {a[2]}")
# 如果使用负数下标,则是从后往前,下标为-1则访问的是最后一个数组元素
print(f"a[-1] = {a[-1]}")
# 如果超过数组的下标访问,则会报错
try:
c = a[10]
except Exception as e:
print("The error message you'll see is:")
# index 10 is out of bounds for axis 0 with size 10
print(e)
# 数组的切分
a = np.arange(10)
# 打印结果为a = [0 1 2 3 4 5 6 7 8 9]
print(f"a = {a}")
# 使用三个数字的, 分别表示 起始位置(包含):结束位置(不包含):步长
# 打印结果为a[2:7:1] = [2 3 4 5 6]
c = a[2:7:1]; print("a[2:7:1] = ", c)
# 打印结果为a[2:7:2] = [2 4 6]
c = a[2:7:2]; print("a[2:7:2] = ", c)
# 使用[起始位置:],则默认访问起始位置(包含)之后的所有元素
# 打印结果为a[3:] = [3 4 5 6 7 8 9]
c = a[3:]; print("a[3:] = ", c)
# 使用[:结束位置],则默认访问结束位置(不包含)之前的所有元素
# 打印结果为a[:4] = [0 1 2 3]
c = a[:4]; print("a[:4] = ", c)
# 打印数组中所有元素
c = a[:]; print("a[:] = ", c)
# 创建数组
a = np.array([1,2,3,4])
# 打印结果为a : [1 2 3 4]
print(f"a : {a}")
# 数组a中的所有元素都取反
b = -a
# 打印结果为b = -a : [-1 -2 -3 -4]
print(f"b = -a : {b}")
# 数组中所有元素的和
b = np.sum(a)
# 打印结果为b = np.sum(a) : 10
print(f"b = np.sum(a) : {b}")
# 数组中元素的平均值
b = np.mean(a)
# 打印结果为b = np.mean(a): 2.5
print(f"b = np.mean(a): {b}")
# 数组中所有元素的二次幂
b = a2
# 打印结果为b = a2 : [ 1 4 9 16]
print(f"b = a2 : {b}")
# 数组间加法,两个数组的元素数量必须一致,否则产生异常
a = np.array([ 1, 2, 3, 4])
b = np.array([-1,-2, 3, 4])
# 打印结果为[0 0 6 8]
print(f"{a + b}")
# 数组每个元素乘以5
a = np.array([1, 2, 3, 4])
b = 5 * a
# 打印结果为b = 5 * a : [ 5 10 15 20]
print(f"b = 5 * a : {b}")
# np.c_运算
# 生成0到5(不包含), 步长为1的一维数组
x = np.arange(0,5,1)
# 将数组x的每一个元素作x, x平方, x立方操作,并形成一个新数组
# 数组x扩张成二维数组X
X = np.c_[x, x2, x3]
# 打印结果为:
# [[ 0 0 0]
# [ 1 1 1]
# [ 2 4 8]
# [ 3 9 27]
# [ 4 16 64]]
print(f"{X}")
点积运算
$x = \sum\limits_{i=0}^{n-1} a_i b_i$
# 使用for循环实现
def my_dot(a, b):
x=0
for i in range(a.shape[0]):
x = x + a[i] * b[i]
return x
# 测试
a = np.array([1, 2, 3, 4])
b = np.array([-1, 4, 3, 2])
# 打印结果my_dot(a, b) = 24
print(f"my_dot(a, b) = {my_dot(a, b)}")
# 使用NumPy的dot函数
a = np.array([1, 2, 3, 4])
b = np.array([-1, 4, 3, 2])
c = np.dot(a, b)
# 简单的测试for循环和NumPy的点积运算速度
np.random.seed(1)
# 生成
a = np.random.rand(10000000)
b = np.random.rand(10000000)
# 使用dot函数
# 起始时间
tic = time.time()
c = np.dot(a, b)
# 结束时间
toc = time.time()
print(f"np.dot(a, b) = {c:.4f}")
print(f"Vectorized version duration: {1000*(toc-tic):.4f} ms ")
# 使用for循环
tic = time.time()
c = my_dot(a,b)
toc = time.time()
print(f"my_dot(a, b) = {c:.4f}")
print(f"loop version duration: {1000*(toc-tic):.4f} ms ")
# 释放大数组的内存
del(a);del(b)
二维数组
# 二维数组
X = np.array([[1],[2],[3],[4]])
w = np.array([2])
c = np.dot(X[1], w)
# 打印结果
# X[1] has shape (1,)
# w has shape (1,)
# c has shape ()
print(f"X[1] has shape {X[1].shape}")
print(f"w has shape {w.shape}")
print(f"c has shape {c.shape}")
多维数组
# 表示创建包含5个元素的1维数组
a = np.zeros((1, 5))
# 打印结果为a shape = (1, 5), a = [[0. 0. 0. 0. 0.]]
print(f"a shape = {a.shape}, a = {a}")
# 表示创建包含1个元素的2维数组
a = np.zeros((2, 1))
# 打印结果为a shape = (2, 1), a = [[0.]
# [0.]]
print(f"a shape = {a.shape}, a = {a}")
# 生成含有1个元素的1维随机数数组
a = np.random.random_sample((1, 1))
# 打印结果为a shape = (1, 1), a = [[0.44236513]]
print(f"a shape = {a.shape}, a = {a}")
# 也可使用如下方法创建
a = np.array([[5], [4], [3]]);
# 使用reshape可方便将1维数组切分为多维数组
# reshape第1个参数表示分成几个数组,如果为-1则表示通过计算自动求得,如果指定了,若和计算求得的不一致,则报错
# reshape第2个参数表示分成的数组中元素的数量
# 下面的式子等价于a = np.arange(6).reshape(3, 2)
a = np.arange(6).reshape(-1, 2)
# 打印结果为a.shape: (3, 2),
# a= [[0 1]
# [2 3]
# [4 5]]
print(f"a.shape: {a.shape}, \na= {a}")
# 访问多维数组的元素,如果是2维数组,则使用两个下标
# 打印结果为4
print(f"\na[2,0] = {a[2,0]}")
# 访问多维数组中的一行,使用一个下标
# 打印结果为a[2].shape: (2,), a[2] = [4 5]
print(f"a[2].shape: {a[2].shape}, a[2] = {a[2]}")
# 多维数组的切分操作
# 2维数组,数组行数2个,每个数组有10个元素
a = np.arange(20).reshape(-1, 10)
# 打印结果为
# a =
# [[ 0 1 2 3 4 5 6 7 8 9]
# [10 11 12 13 14 15 16 17 18 19]]
print(f"a = \n{a}")
# 访问第一行的数组(下标为0), 切分规则和一维数组相同
print("a[0, 2:7:1] = ", a[0, 2:7:1], ", a[0, 2:7:1].shape =", a[0, 2:7:1].shape, "a 1-D array")
# 访问多维数组中所有数组, 并且进行切分
print("a[:, 2:7:1] = \n", a[:, 2:7:1], ", a[:, 2:7:1].shape =", a[:, 2:7:1].shape, "a 2-D array")
# 访问多维数组中的所有元素
print("a[:,:] = \n", a[:,:], ", a[:,:].shape =", a[:,:].shape)
# 访问下标为1的数组的所有元素
print("a[1,:] = ", a[1,:], ", a[1,:].shape =", a[1,:].shape, "a 1-D array")
# a[1,:]可以简写为a[1]
print("a[1] = ", a[1], ", a[1].shape =", a[1].shape, "a 1-D array")
多元线性回归
使用矢量化后的多元线性回归中的梯度下降

注意图中的带箭头表示矢量的参数.

特别注意参数w的梯度下降中导数中的$x^{(i)}_i$参数也是随着w而变化的.
代码
有四个特征的训练集
X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
y_train = np.array([460, 232, 178])
初始化矢量w和数字b的值
b_init = 785.1811367994083
# 矢量w有四个特征
w_init = np.array([ 0.39133535, 18.75376741, -53.36032453, -26.42131618])
模型函数
$$ f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b \tag{4} $$
成本函数
$$J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 \tag{3}$$
计算成本
def compute_cost(X, y, w, b):
"""
成本函数计算
参数:
X: 特征数组
y: 目标数据数组
w: 模型参数w数组
b: 模型参数b数字
返回:
cost: 成本
"""
m = X.shape[0]
cost = 0.0
for i in range(m):
# 使用点积运算快速计算函数f
f_wb_i = np.dot(X[i], w) + b
cost = cost + (f_wb_i - y[i])2
cost = cost / (2 * m)
return cost
# 进行调用
cost = compute_cost(X_train, y_train, w_init, b_init)
# 打印结果为Cost at optimal w : 1.5578904045996674e-12
print(f'Cost at optimal w : {cost}')
梯度下降
$$\begin{align*} \text{repeat}&\text{ until convergence:} ; \lbrace \newline; & w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{5} ; & \text{for j = 0..n-1}\newline &b\ \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{align*}$$
其中导数部分 $$ \begin{align} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \tag{6} \ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{7} \end{align} $$ 公式(6), (7)代码:
def compute_gradient(X, y, w, b):
# m记录数据数量, n是特征数量
m, n = X.shape
dj_dw = np.zeros((n,))
dj_db = 0.
for i in range(m):
# 计算都使用到的部分
item = (np.dot(X[i], w) + b) - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + item * X[i, j]
dj_db = dj_db + item
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
公式(5)代码
def gradient_descent(X, y, w_in, b_in, cost_fuction, gradient_function, alpha, num_iters):
"""
参数alpha是学习率
num_iters是迭代次数
返回值有:
w: 特征参数数组
b: 参数b的值
J_history: 计算函数J的历史值数组
"""
J_history = []
w = copy.deepcopy(w_in)
b = b_in
for i in range(num_iters):
# 取出计算的线性导数值
dj_dw, dj_db = gradient_function(X, y, w, b)
w = w - alpha * dj_dw
b = b - alpha * dj_db
if i < 100000:
J_history.append(cost_function(X, y, w, b))
if i % math.ceil(num_iters/10) == 0:
print(f"Iteration {i:4d}: Cost {J_history[-1]:8.2f} ")
return w, b, J_history
# 调用和测试
initial_w = np.zeros_like(w_init)
initial_b = 0.
# 循环次数
iterations = 1000
# 学习率
alpha = 5.0e-7
# 调用
w_final, b_final, J_hist = gradient_descent(X_train, y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations)
# 显示最终的参数b和w
print(f"b,w found by gradient descent: {b_final:0.2f},{w_final} ")
m,_ = X_train.shape
# 打印使用训练好的参数m和b和实际的值进行比较
for i in range(m):
print(f"prediction: {np.dot(X_train[i], w_final) + b_final:0.2f}, target value: {y_train[i]}")
特征缩放
为何使用特征缩放
当有不同的特征, 且它们的取值范围非常不同时, 可能会导致梯度下降运行缓慢. 如果重新缩放不同的特征, 使它们都具有可比较的取值范围, 从而让运行速度, 升级, 特征显著.
如果预测房价的模型是如下图:

尺寸和房价数量的取值范围相差巨大, 直观感受图:
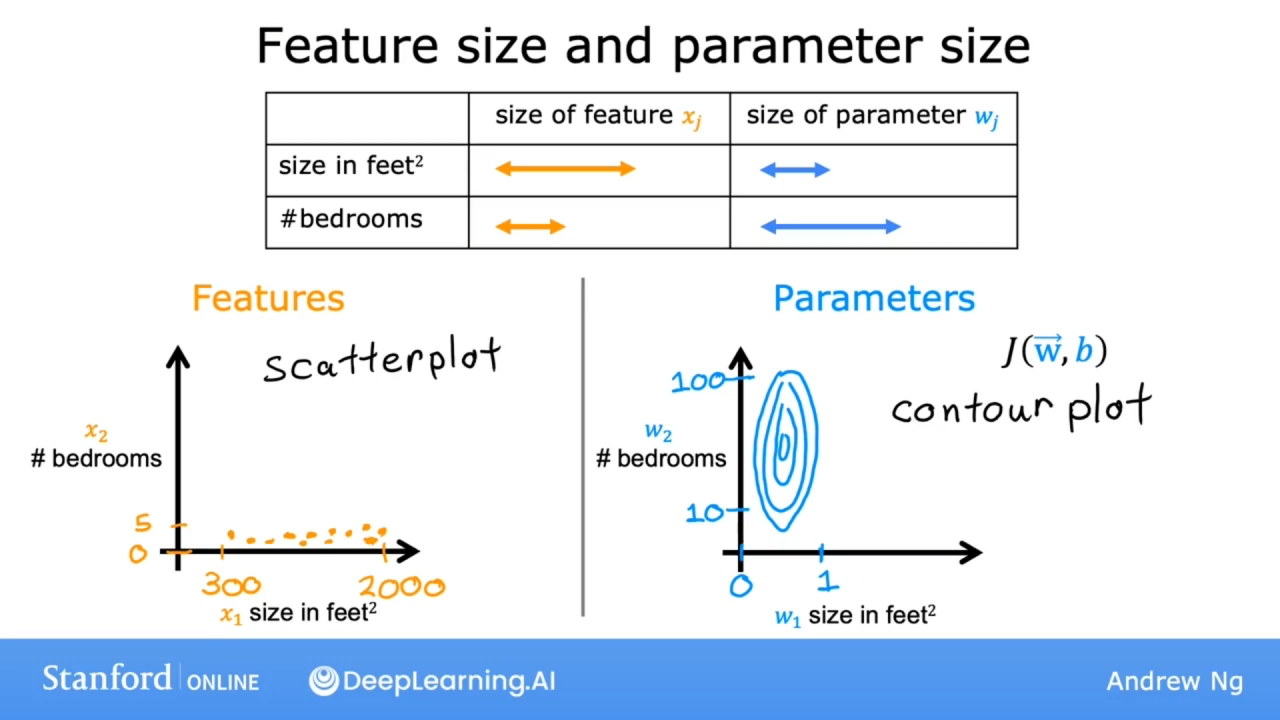
通过上图可看出, 特征不同会造成数据点不均匀, 也导致成本函数J的等高线图的同心曲线不怎么接近圆形, 一侧较短, 一侧较长.
对w1的非常小的变化会对估计价格产生非常大的影响, 也对成本函数J的影响大, 因为w1的往往会乘以一个非常大的数(特征的取值范围大).
相比之下, w2需要更大的变化才能大大改变预测的价格, 对成本函数的影响比较小.
这样会导致:
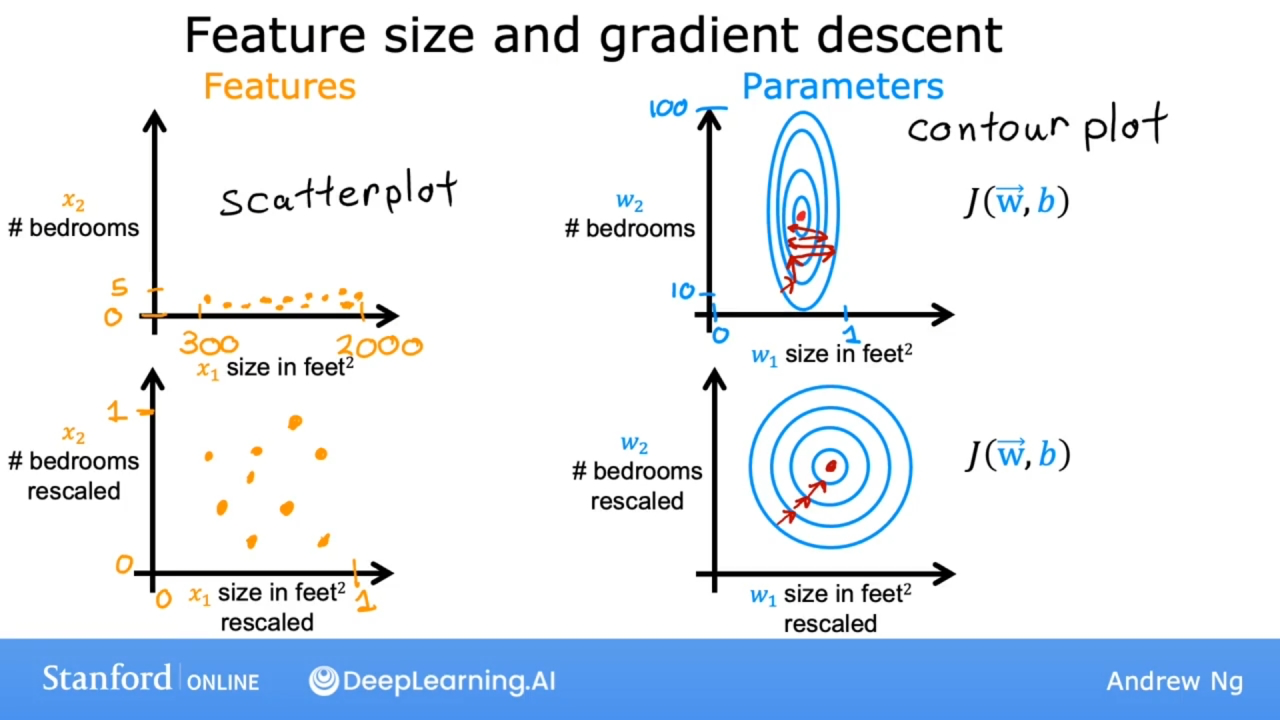
等高线又高又瘦, 梯度下降可能会在它最终找到全局最小值之前来回弹跳很长时间.
使用特征缩放后, 梯度下降可以找到一条更直接的通往全局最小值的路径.
特征缩放的几种方式
最大值法
使用特征的取值范围的最大值, 作为分布, 对特征进行缩放, 如下图

均值归一化
Mean normalization
找到特征的平均值$\mu$, 使用公式$x = \frac {x - \mu} {max - min}$进行缩放

Z-Score归一化
要实现z-score归一化, 需要计算每个特征的标准差$\sigma$和平均值$\mu$, 使用公式$x = \frac {x - \mu} {\sigma}$进行缩放
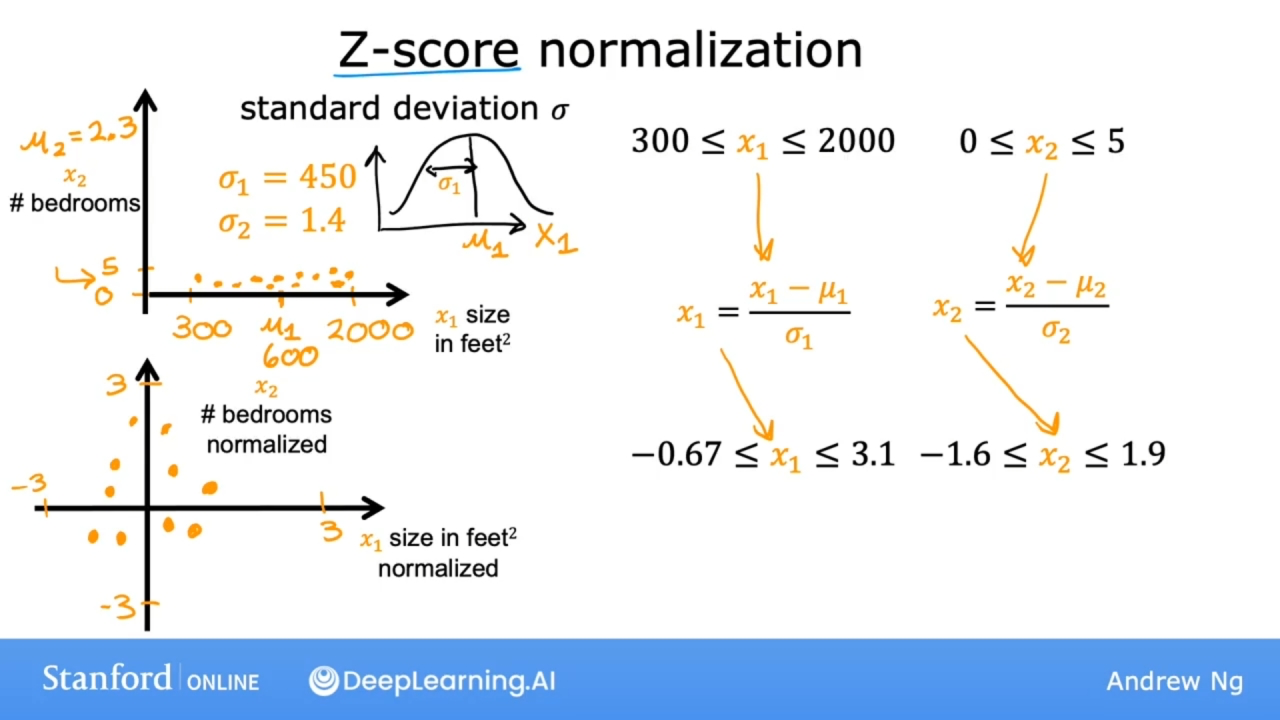
如何计算标准差?
使用图上所示的正态分布
代码
实现Z-Score归一化
$$x^{(i)}_j = \dfrac{x^{(i)}_j - \mu_j}{\sigma_j} \tag{4}$$
其中$\mu_j$和$\sigma_j$由以下公式获得 $$ \begin{align} \mu_j &= \frac{1}{m} \sum_{i=0}^{m-1} x^{(i)}j \ \sigma^2_j &= \frac{1}{m} \sum{i=0}^{m-1} (x^{(i)}_j - \mu_j)^2 \end{align} $$
def zscore_normalize_features(X):
# 把训练集中的所有特征数据都进行计算
# axis=0为纵向,相当于取二维数组中的一维数组中的下标相同的元素进行操作
# axis=1为横向,相当于取二维数组中的一维数组中所有元素进行操作
mu = np.mean(X, axis=0)
sigma = np.std(X, axis=0)
X_norm = (X - mu) / sigma
return (X_norm, mu, sigma)
度量特征缩放
缩放后的特征数据在一个数量级时是可接受的, 如下图

梯度下降收敛
如何判断梯度下降工作正确

通过观察迭代次数和成本函数J的曲线图, 成本函数J应该在每次迭代后减少. 如果增加, 意味着学习率$\alpha$选择不当或者代码中可能存在错误.
如果如上图那样平滑的下降, 并且在迭代到某个次数时不再有大的变化, 则此时梯度下降工作正确.
如上图, 可判断出在迭代400次后, 成本函数J收敛(converged). 不同的应用程序的收敛的迭代次数千差万别.
还有一个使用自动收敛测试的方法(但不推荐):
给定一个阈值$\epsilon$, 如果每次迭代成本函数的减少小于此变量, 则可声明收敛. 但选择正确的阈值$\epsilon$非常困难.
选择正确的学习率
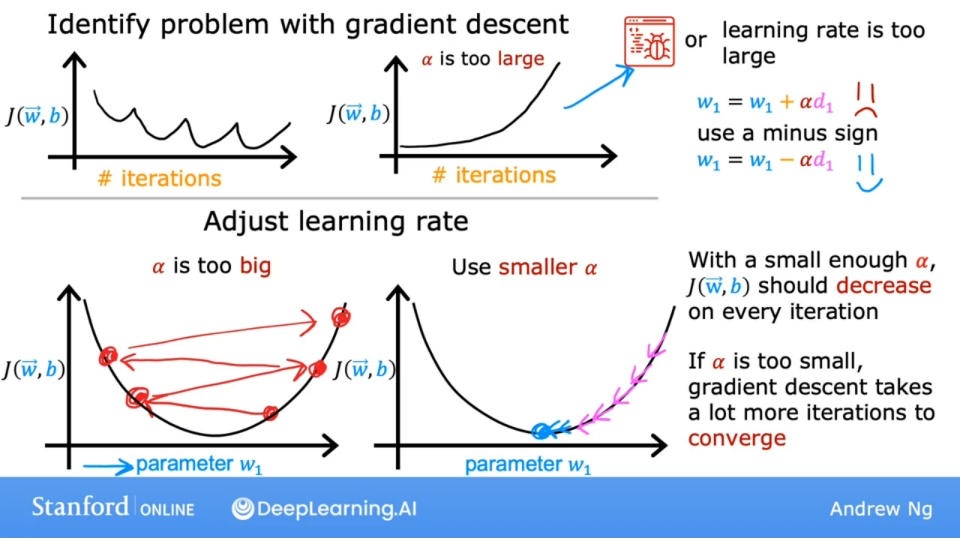
如果发现成本函数J不是随着迭代次数下降, 则有可能是学习率选择不当, 或是代码有错误, 如何区分呢?
正确实施梯度下降的一个调试技巧是, 如果学习率足够小, 成本函数应该在每次迭代中减少. 如果梯度下降不起作用, (调试经验)将学习率设置为一个非常小的数字, 看是否在每次迭代时导致成本下降.
如果将学习率设置为非常小的数字, 成本函数J也不会在每次迭代中减少, 而有时会增加, 那么通常意味着代码中某处存在错误(如图中的把减号写成加号).
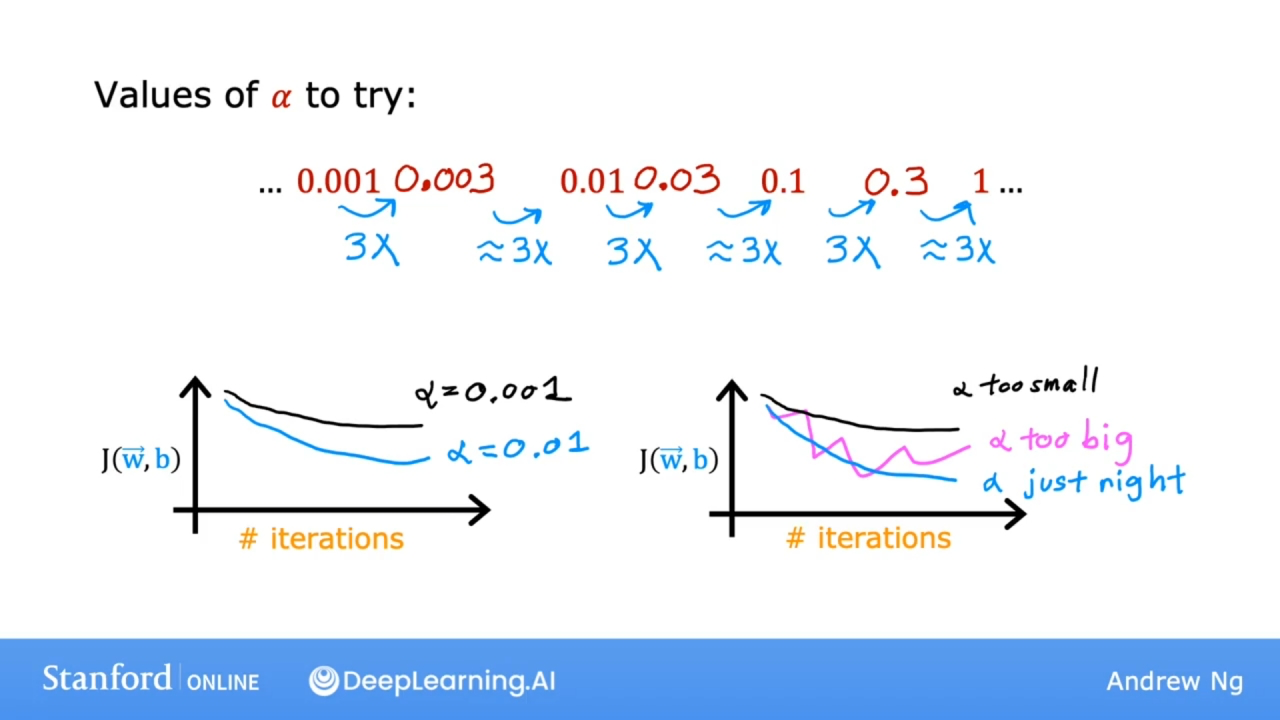
依次尝试学习率为...0.001, 0.01, 0.1, 1... 如果找到了让成本函数J下降到上升的边界, 则尝试用最小学习率. 通过每次乘以3倍的重试, 找到比较符合成本函数下降最快的学习率.
特征工程
Feature engineering
对于许多实际应用而言, 选择或输入正确的特征是使算法良好运行的关键.
可以利用对问题的知识或直觉来设计新特征, 通常是转换或组合问题的原始特征来使学习算法更容易做出准确的预测.
英文定义:
Using intuition(直觉) to design new features, by transforming or combining original features.
多项式回归
Polynomial regression
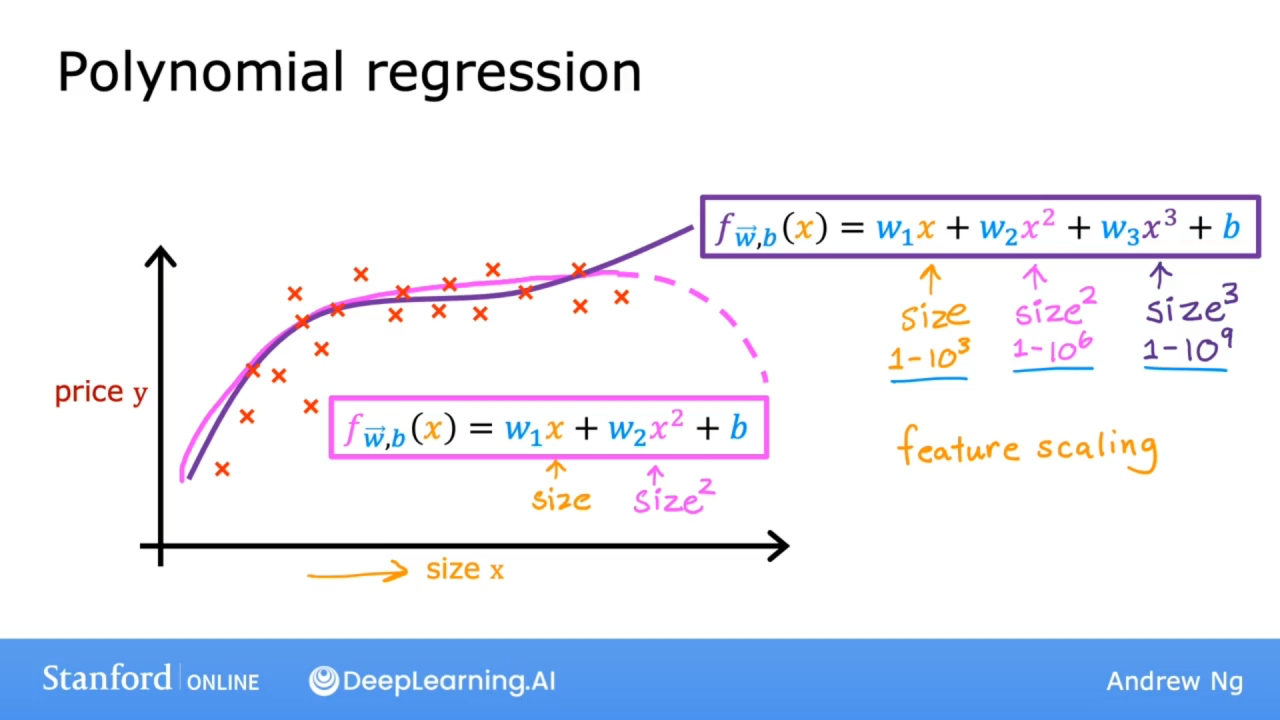
为了更切合训练数据, 可能会使用多项式, 而二次幂会随着特征值的增加而降低, 这显然是不符合逻辑的, 因此加入了三次幂来预测.
如果是图上的多次项, 那么特征缩放会越来越重要, 因为特征数据的范围会随着多次幂急剧增加.
还有一种合理的替代方案, 使用特征的平方根, 平方根函数随着特征的增加, 曲线不会那么陡峭, 但永远不会变平, 而且肯定永远不会回落.
使用Scikit-Learn
文档地址: https://scikit-learn.org/stable/index.html
代码
# 导入库
import numpy as np
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.preprocessing import StandardScaler
# 加载训练集
X_train, y_train = load_house_data()
# 特征缩放
scaler = StandardScaler()
X_norm = scaler.fit_transform(X_train)
# 创建和调整回归模型
sgdr = SGDRegressor(max_iter=1000)
sgdr.fit(X_norm, y_train)
# 训练出来的模型参数
b_norm = sgdr.intercept_
w_norm = sgdr.coef_
# 做出预测,y_pred_sgd是预测值,y_pred是目标值
y_pred_sgd = sgdr.predict(X_norm)
y_pred = np.dot(X_norm, w_norm) + b_norm
分类算法
只有两种可能输出的分类问题称为二元分类(binary classification).
通常将否定结果的称为negative class, 正确结果的称为positive class.
线性回归不能很好的运用于分类问题, 如下图:
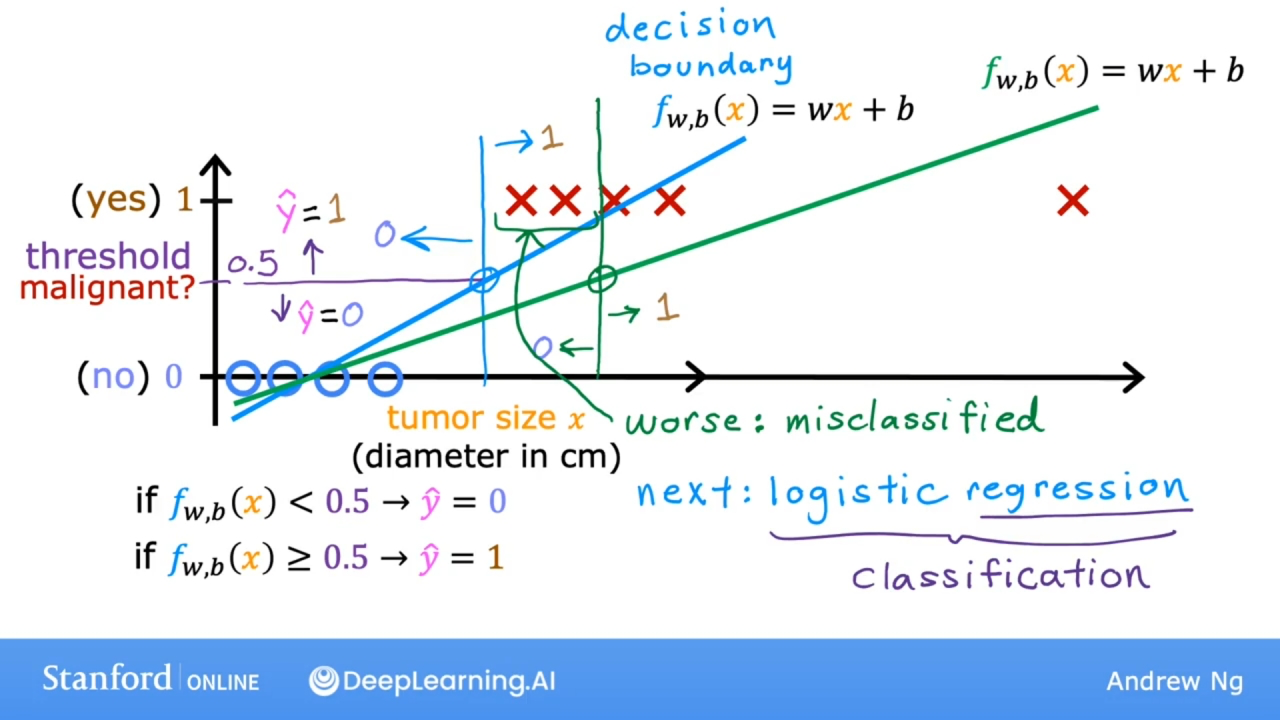
如上图使用阈值0.5来预测是否是肿瘤. 阈值0.5称为决策边界(decision boundary).
如图所示, 如果右边添加了一个训练数据, 会导致线性模型函数f向右倾斜, 决策边界向右移动. 导致原来预测为恶性的, 现在变为良性.
使用逻辑回归(logistic regression)算法解决分类问题.
逻辑回归
Logistic regression
描述
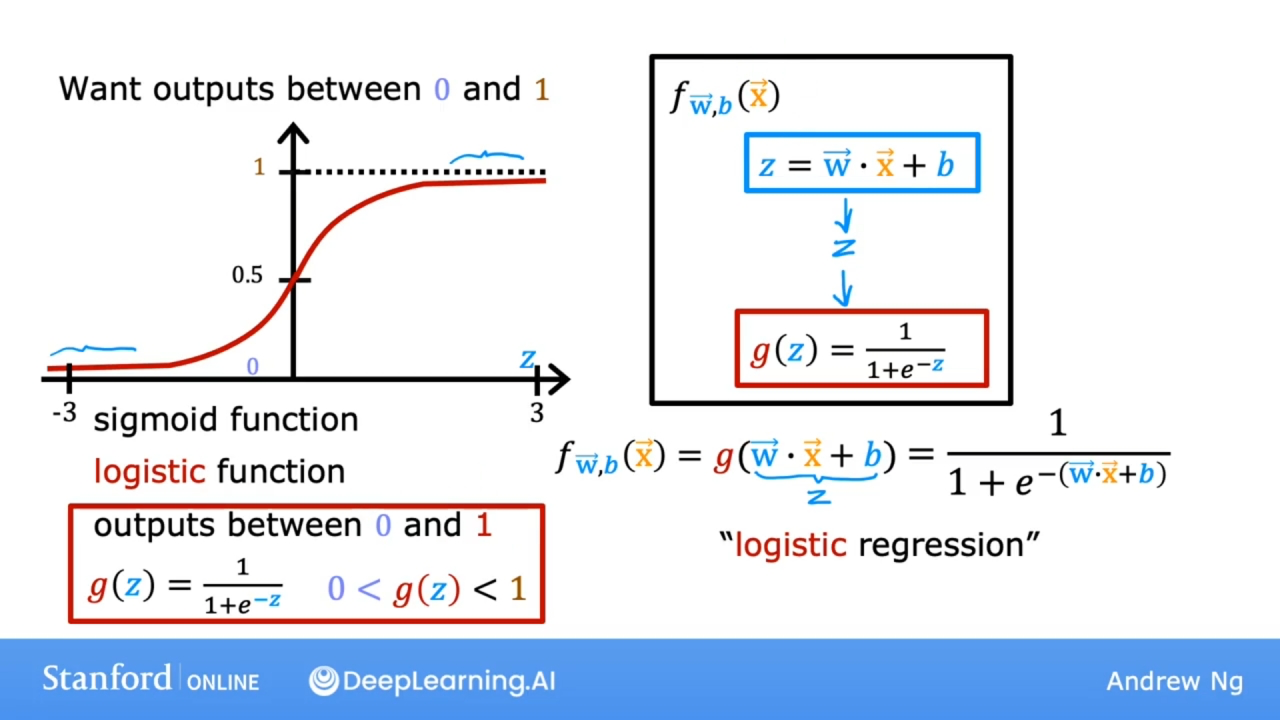
使用sigmoid 函数(也叫逻辑函数-logistic function)解决分类问题.
$g(z) = \frac{1}{1+e^{-z}}$ 其中$e$是自然参数, 此函数的曲线如上图所示.
若有线性模型f, 使$z = \mathbf{w} \cdot \mathbf{x} + b$ 代入到sigmoid函数中, 可得: $$ f_{\mathbf{w},b}(\mathbf{x}) = g(\mathbf{w} \cdot \mathbf{x} + b ) = \frac{1}{1+e^{-(\mathbf{w} \cdot \mathbf{x} + b)}} $$ 逻辑回归的输出描述:
在给定输入特征数据的情况下输出类或标签等于1(正确结果)的概率.
概率公式: $P(y = 0) + P(y = 1) = 1$, 其中P是概率.
假如输出的结果是0.8, 则说明有80%的几率有恶性肿瘤的风险.
有时会表示为如下公式: $$ f_{\mathbf{w},b}(\mathbf{x}) = P(y=1|\mathbf{x};\mathbf{w},b) $$ 公式描述: f的值为给定输入的特征x和参数w, b, y=1的概率.
代码
sigmoid函数的实现: $g(z) = \frac{1}{1+e^{-z}}$
# 导入NumPy库
import numpy as np
# 使用np.exp()函数获取自然参数e的值
# 但只有一个输入值,且为1时
input_val = 1
# 相当于e的input_val幂
exp_val = np.exp(input_val)
# 输出结果为Output of exp: 2.718281828459045
print("Output of exp:", exp_val)
# 传入数组
input_array = np.array([1,2,3])
exp_array = np.exp(input_array)
# 输出结果为Output of exp: [ 2.72 7.39 20.09]
print("Output of exp:", exp_array)
# 实现sigmoid函数
def sigmoid(z):
g = 1 / (1 + np.exp(-z))
return g
决策边界
Decision boundary
描述
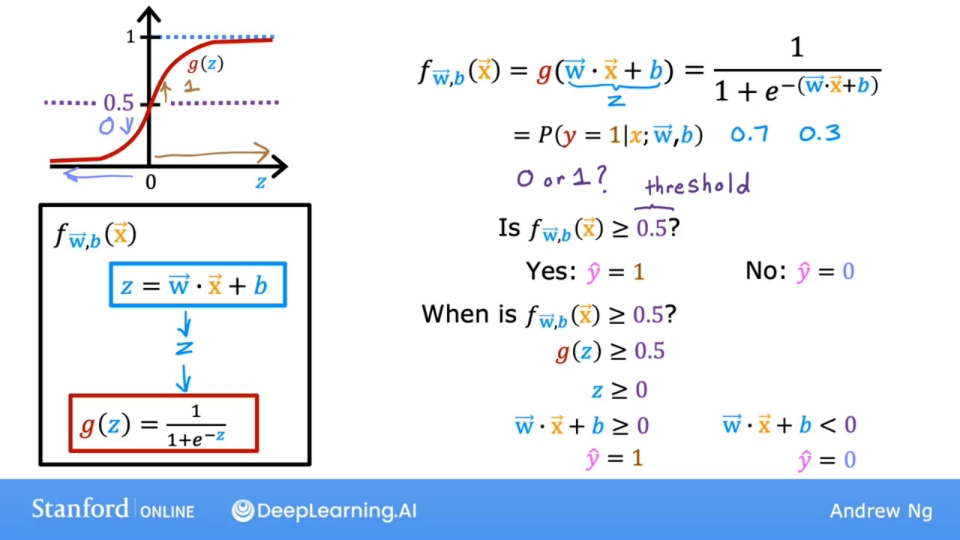
如上图, 如果选择阈值为0.5, 则当模型函数$f >= 0.5$ 时, 预测的y值为1(yes, 正确结果). 有以下公式: $$ z = \mathbf{w} \cdot \mathbf{x} + b \newline f_{\mathbf{w},b}(\mathbf{x}) = g(z) = \frac{1}{1+e^{-(\mathbf{w} \cdot \mathbf{x} + b)}} $$ 也就是$g(z) >= 0.5$ 于是得出 $z >= 0$ 因此有 $\mathbf{w} \cdot \mathbf{x} + b >= 0$
可视化
决策边界就是让 $z = \mathbf{w} \cdot \mathbf{x} + b = 0$ 的曲线
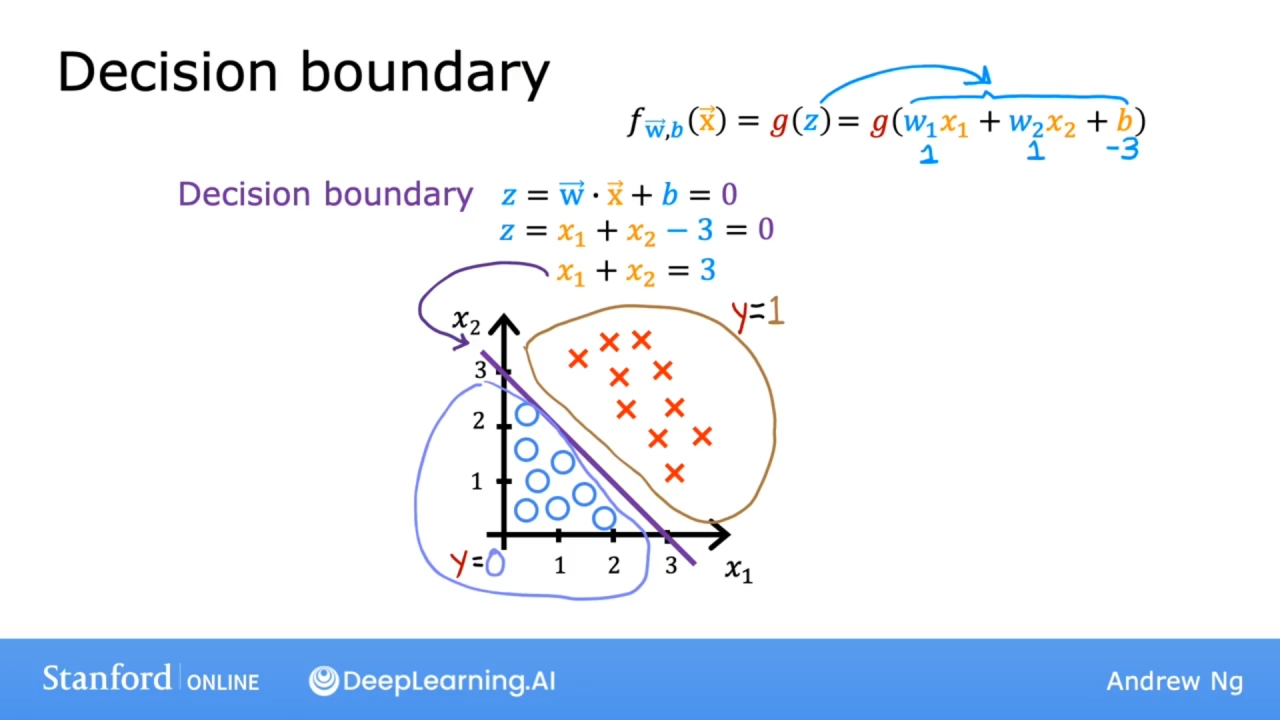
上图时两个特征的决策边界, 是一条直线.

上图时二次多项式下的两个特征的决策边界, 是一个圆.
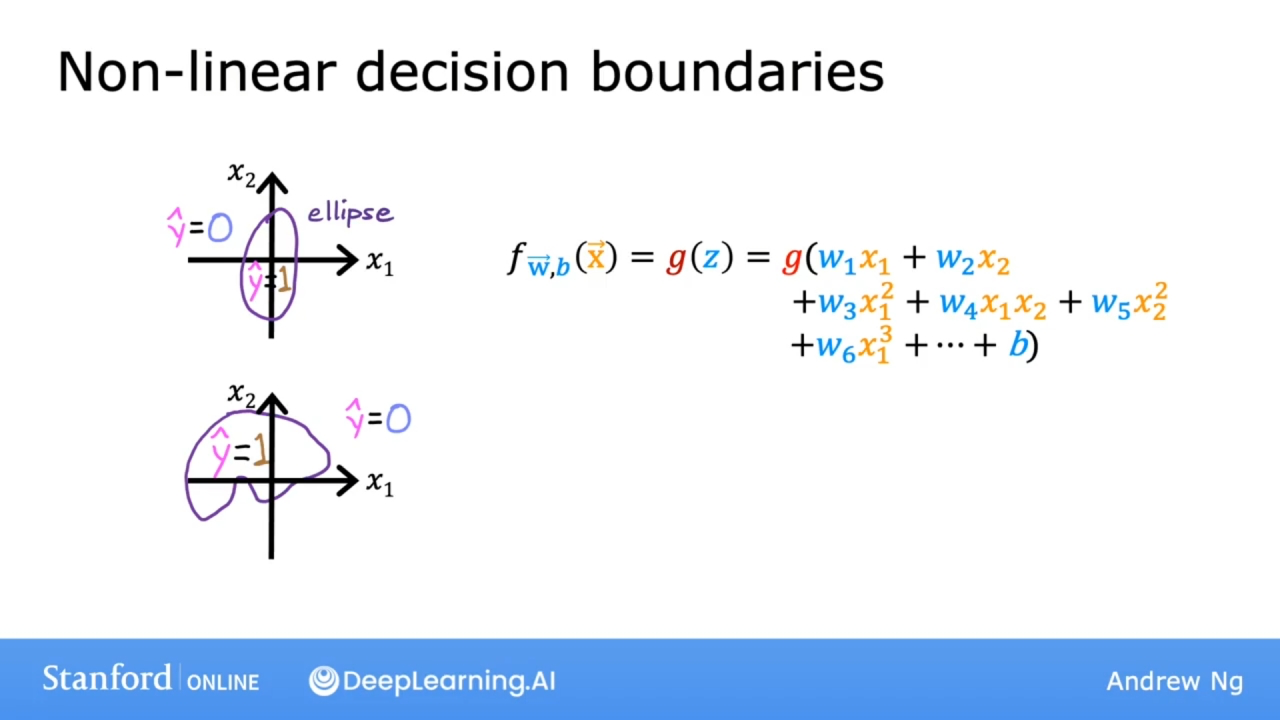
上图时多次多项式下的多个特征的决策边界, 是复杂的曲线.
逻辑回归的成本函数
对于逻辑回归使用误差平方成本函数(squared error cost)不是很好的选择, 如下图:

如果使用误差平方成本函数, 则在逻辑回归中, 曲线如上图所示, 则成本函数J将会有很多的局部最小值. 不是一个凸函数曲线.
图中的 $\frac{1}{2}(f_{w,b}(x^{(i)}) - y^{(i)})^2$ 称作单个训练数据中的损失(loss), 记作:$L(f_{w,b}(x^{(i)}), y^{(i)})$
损失函数衡量的是在一个训练样例的表现如何, 成本函数衡量的是在整个训练集是那个的表现.
通过给损失函数选择不同的形式, 将能够保持总成本函数成为一个凸函数.
公式

上图展示的是损失函数当 $y^{(i)} = 1$ 的情况
函数$-log(f)$的曲线如图所示, 因模型函数f的取值范围是[0, 1], 因此只看此函数$-log(f)$在区间[0, 1]的曲线.
如果模型函数f的值趋近于1, 则损失函数趋近于0.
如果模型函数f的值取经于0, 则损失函数趋近于无穷.
因此当 $y^{(i)} = 1$ 时, 损失函数会帮助算法做出更准确的预测, 因为当预测值接近1时, 此时的损失最小.
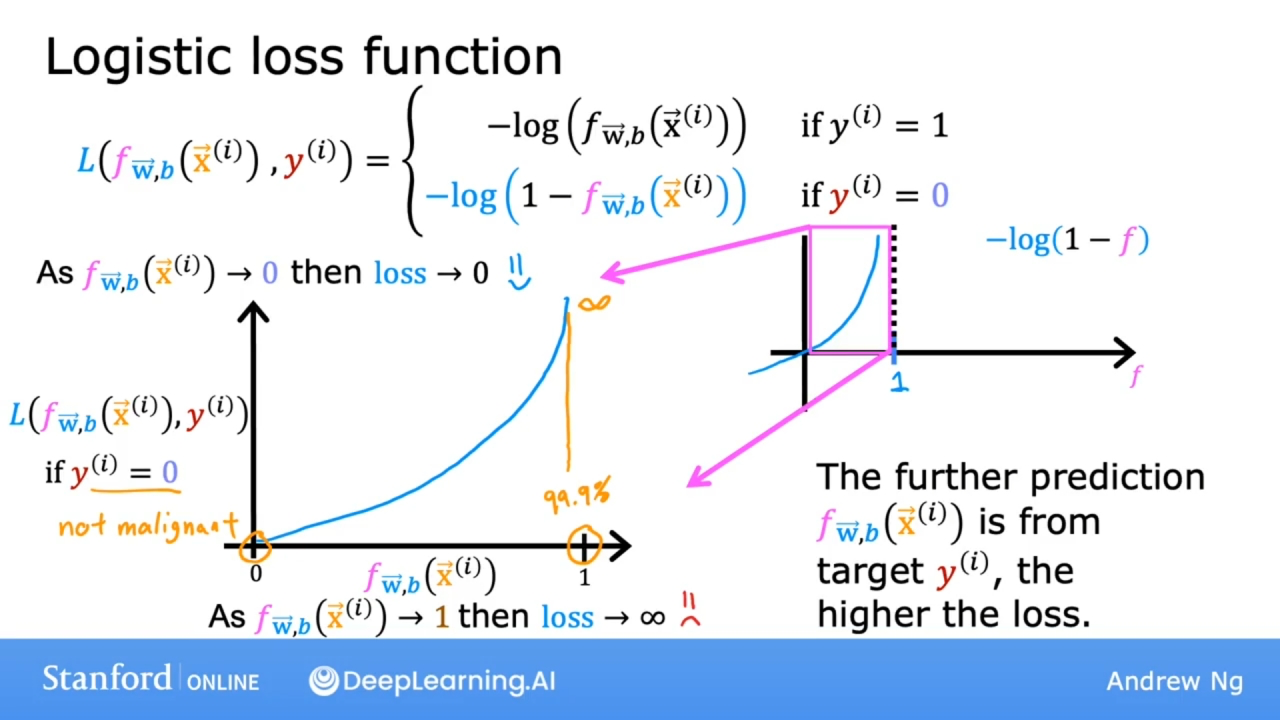
上图展示的是损失函数当 $y^{(i)} = 0$ 的情况
函数$-log(1-f)$的曲线如图所示, 因模型函数f的取值范围是[0, 1], 因此只看此函数$-log(1-f)$在区间[0, 1]的曲线.
如果模型函数f的值趋近于1, 则损失函数趋近于无穷.
因此当 $y^{(i)} = 0$ 时, 损失函数会帮助算法做出更准确的预测, 因为当预测值接近1时, 此时损失非常高.
通过上面两种损失函数的选择, 整体成本函数将是凸函数, 可以可靠地使用梯度下降达到全局最小值.
损失函数
$loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)})$ $$ \begin{equation} loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) = \begin{cases} - \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) & \text{if $y^{(i)}=1$}\ \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) & \text{if $y^{(i)}=0$} \end{cases} \end{equation} $$ 通用公式 $$ loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) = (-y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) $$ 当 $y^{(i)} = 0$ 时 $$ \begin{align} loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), 0) &= (-(0) \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - 0\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) \ &= -\log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) \end{align} $$ 当 $y^{(i)} = 1$ 时 $$ \begin{align} loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), 1) &= (-(1) \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - 1\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right)\ &= -\log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) \end{align} $$
成本函数
成本函数
$$ J(\mathbf{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) \right] \tag{1}$$
损失函数
$$loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) = -y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) \tag{2}$$
其中模型函数f和sigmoid函数 $$ \begin{align} f_{\mathbf{w},b}(\mathbf{x^{(i)}}) &= g(z^{(i)}) \ z^{(i)} &= \mathbf{w} \cdot \mathbf{x}^{(i)}+ b \ g(z^{(i)}) &= \frac{1}{1+e^{-z^{(i)}}} \end{align} $$ 这个特定的成本函数是使用称为最大似然估计(maximum likelihood)的统计原理从统计中推导出来的.
成本函数代码
def compute_cost_logistic(X, y, w, b):
"""
参数:
X: 训练集,包含多个特征
y: 目标值
w: 模型参数,有多个
b: 模型参数
"""
m = X.shape[0]
cost = 0.0
for i in range(m):
# 计算函数g(z)的z值
z_i = np.dot(X[i], w) + b
# 代入函数g(z)中
f_wb_i = 1 / (1 + np.exp(-z_i))
# 计算损失函数
loss_i = -y[i] * np.log(f_wb_i) - (1 - y[i]) * np(1 - f_wb_i)
# 所有损失函数之和
cost = cost + lost_i
# 最后除以训练集数据数量m
cost = cost / m
return cost
实现梯度下降

如上图显示的公式, 是不是和线性回归的梯度下降表达式相似?
但逻辑回归的模型函数f是 $f_{\mathbf{w},b}(\mathbf{x}) = \frac{1}{1+e^{-(\mathbf{w} \cdot \mathbf{x} + b)}}$
而线性回归的模型函数f是 $$f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w} \cdot \mathbf{x} + b$$
如下图所示:

逻辑回归同样可以使用:
- 监控梯度下降(学习率曲线)
- 矢量化运算
- 特征缩放
梯度下降代码
实现梯度下降中的repeat代码块部分
def compute_gradient_logistic(X, y, w, b):
m,n = X.shape
# 注意参数w是特征数量n个,因此使用np的数组初始化
dj_dw = np.zeros((n,))
dj_db = 0.0
for i in range(m):
z_i = np.dot(X[i], w) + b
# 计算函数f
f_wb_i = 1 / (1 + np.exp(-z_i))
# 计算函数f和目标值y的差值
dj_db_i = f_wb_i - y[i]
# 计算每个特征对应的参数w的值
for j in range(n):
dj_dw[j] = dj_dw[j] + dj_db_i * X[i, j]
# 计算参数b的值
dj_db = dj_db + dj_db_i
# 最后不忘除以训练集的数量m
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
实现逻辑回归的梯度下降
def gradient_descent(X, y, w_in, b_in, alpha, num_iters):
# 存储成本函数J的历史值
J_history = []
w = copy.deepcopy(w_in)
b = b_in
for i in range(num_iters):
# 通过调用函数获取dj_dw, dj_db
dj_dw, dj_db = compute_gradient_logistic(X, y, w, b)
# 梯度下降
w = w - alpha*dj_dw
b = b - alpha*dj_db
# 记录成本函数
if (i < 100000):
J_history.append(compute_cost_logistic(X, y, w, b))
# 打印一些统计信息
if i% math.ceil(num_ites/10) == 0:
print(f"Iteration {i:4d}: Cost {J_history[-1]} ")
return w, b, J_history
使用Scikit-Learn
可使用Scikit-Learn直接封装好的逻辑回归
# 导入库
import numpy as np
from sklearn.linear_model import LogisticRegression
# 训练集
X = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
# 目标值
y = np.array([0, 0, 0, 1, 1, 1])
# 创建逻辑回归模型
lr_model = LogisticRegression()
# 适配模型数据
lr_model.fit(X, y)
# 根据训练集进行预测
y_pred = lr_model.predict(X)
# 打印预测结果
print("Prediction on training set:", y_pred)
# 打印预测的分数-准确率
print("Accuracy on training set:", lr_model.score(X, y))
过拟合问题
描述
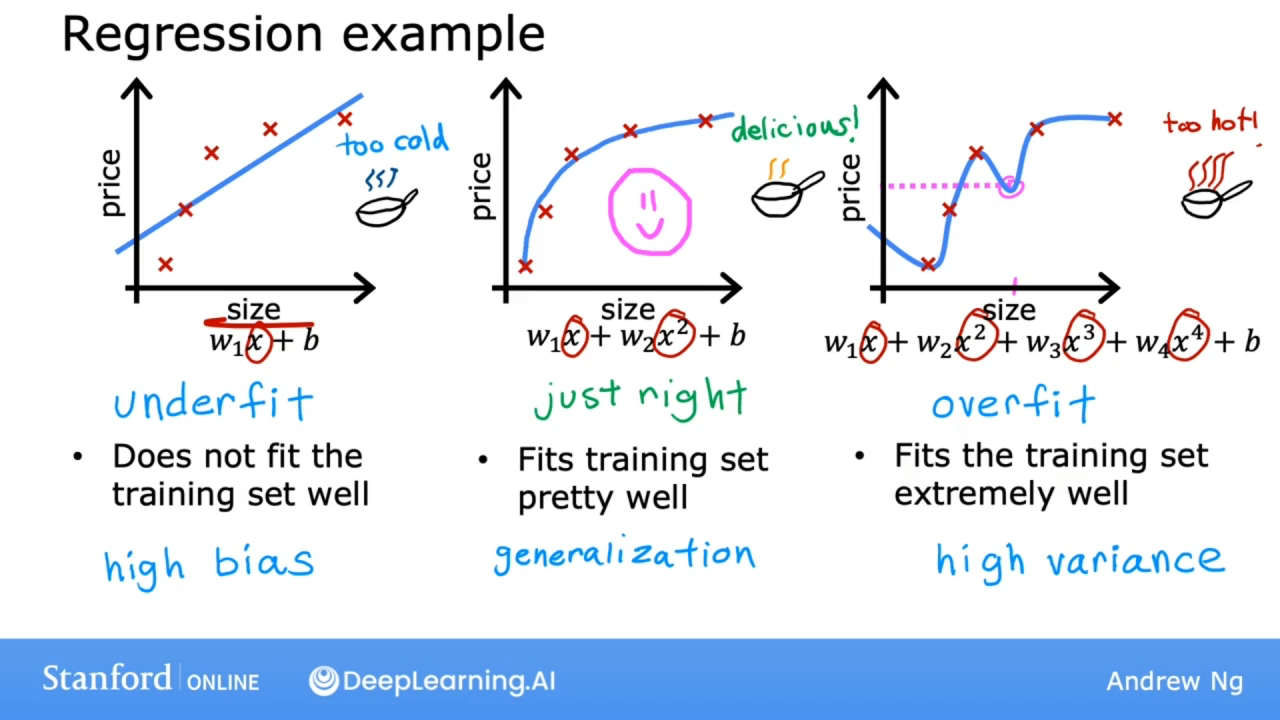
对于如上图的模型, 过度的切合训练数据会造成过拟合(overfit)问题.
上图左边的模型对训练数据是欠拟合(underfit)的, 或算法具有高偏差(high bias).
中间的模型对训练数据切合的比较不错, 并且此算法能够很好地进行泛化(generalization), 这意味着即使模型在全新从未见过的数据上也能够做出良好的预测.
右边的模型对训练数据极度的适合, 并且完美通过了所有的训练数据.
- 但当在全新的数据上做出的预测是不正确的(比如图中粉色部分, 房子尺寸大了, 反而价格降低了), 这个模型对数据过度拟合(overfit), 或说这个算法具有高方差(high variance).
- 这个模型不会推广到从未见过的新数据上. 如果训练集有一点点不同, 那么该算法拟合的函数最终可能会完全不同.
- 如果讲模型拟合到略有不同的数据集, 就会得到完全不同的预测或高度可变的预测, 即该算法具有高方差.
对于分类模型, 也有如下的问题:

解决方法
收集更多的训练数据
通过收集更多的训练数据, 学习算法将学会适应一个波动较小的函数.
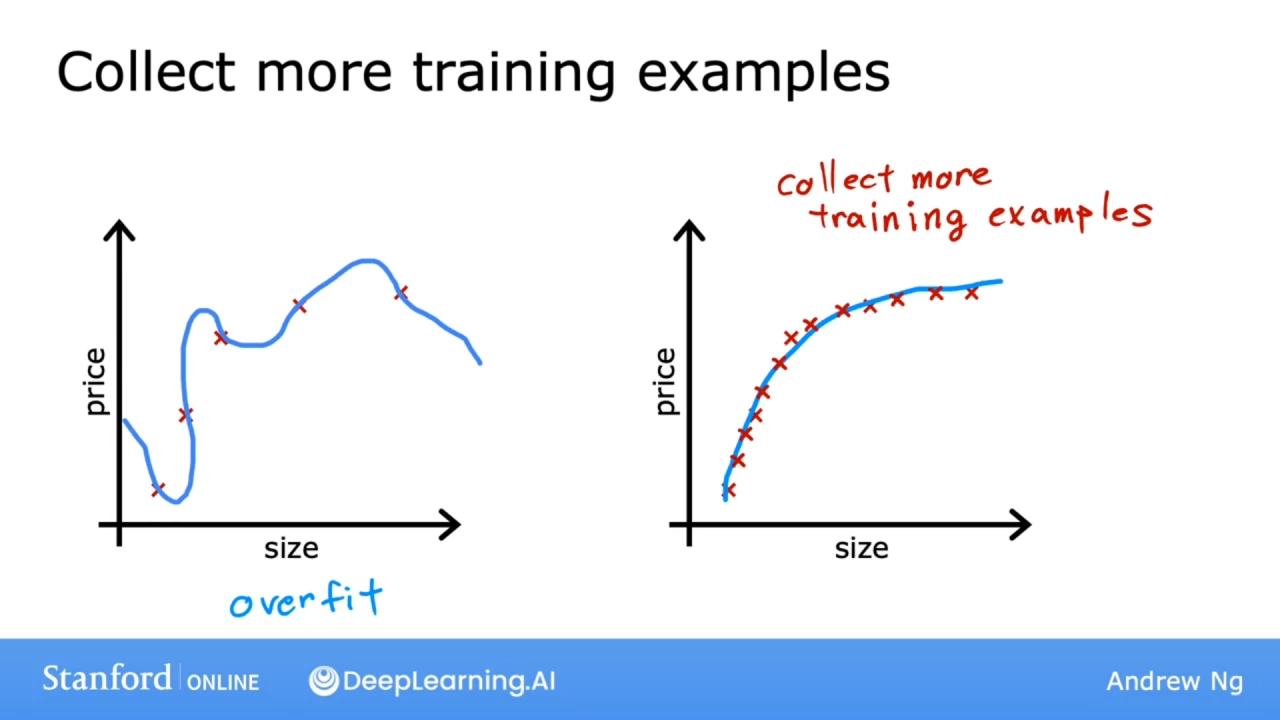
但在实际中通常是比较困难的.
选择特征
使用太多多项式特征, 也可能会造成过拟合问题.
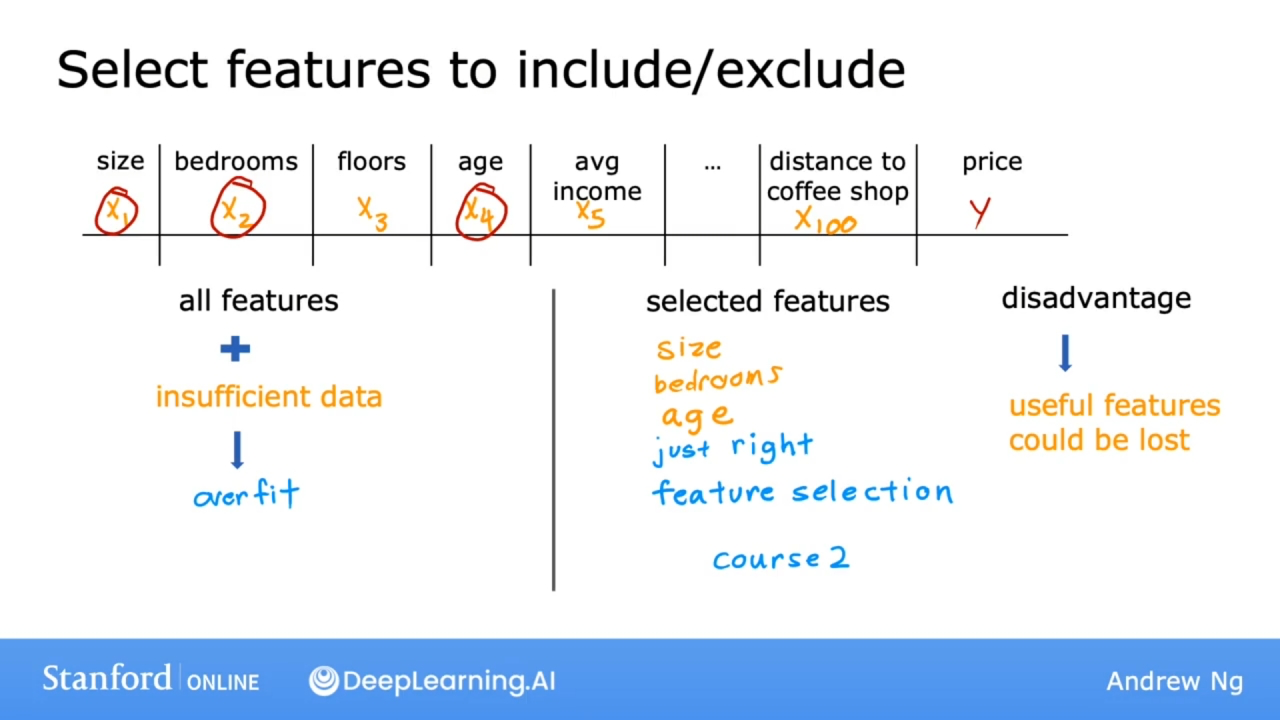
选择最合适的一组特征来使用, 称为特征选择(feature selection). 关于特征选择, 将在第二课中讲解.
特征选择的一个缺点: 假如所有的特征实际上都可用于预测, 仅使用特征的一个子集, 该算法会丢弃有关的一些信息.
正则化
Regularization
如果要消除某一个特征, 有可能把这个特征的参数设置为0, 正则化是一种更温和地减少某些特征影响的方法, 而不用像彻底消除那样严厉.
正则化的作用是鼓励学习算法缩小参数值, 而不必要求参数正好设置为0.
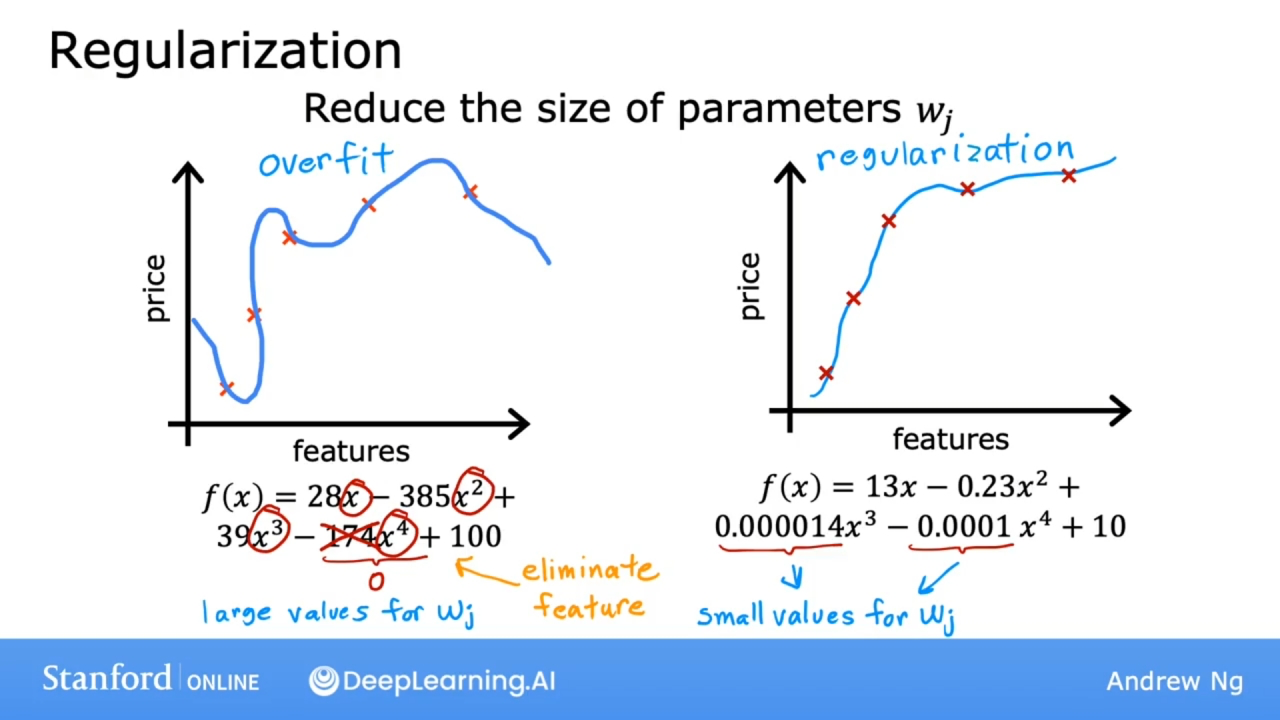
正则化的作用是可以让你保留所有特征, 但防止特征产生过大的影响, 因为有时会导致过度拟合.
是否对参数b进行正则化并没有太大区别, 推荐不正则化参数b.
应用正则化
原理
一般地说, 正则化的实现方式是, 如果有很多特征, 不知道哪些是最重要的特征, 哪些是要惩罚的特征, 正则化的典型实现方式是惩罚所有的特征, 即惩罚所有的$w_j$参数, 并且有可能表明这通常会导致拟合更平滑, 更简单, 周期更少的函数, 也不太容易过度拟合.
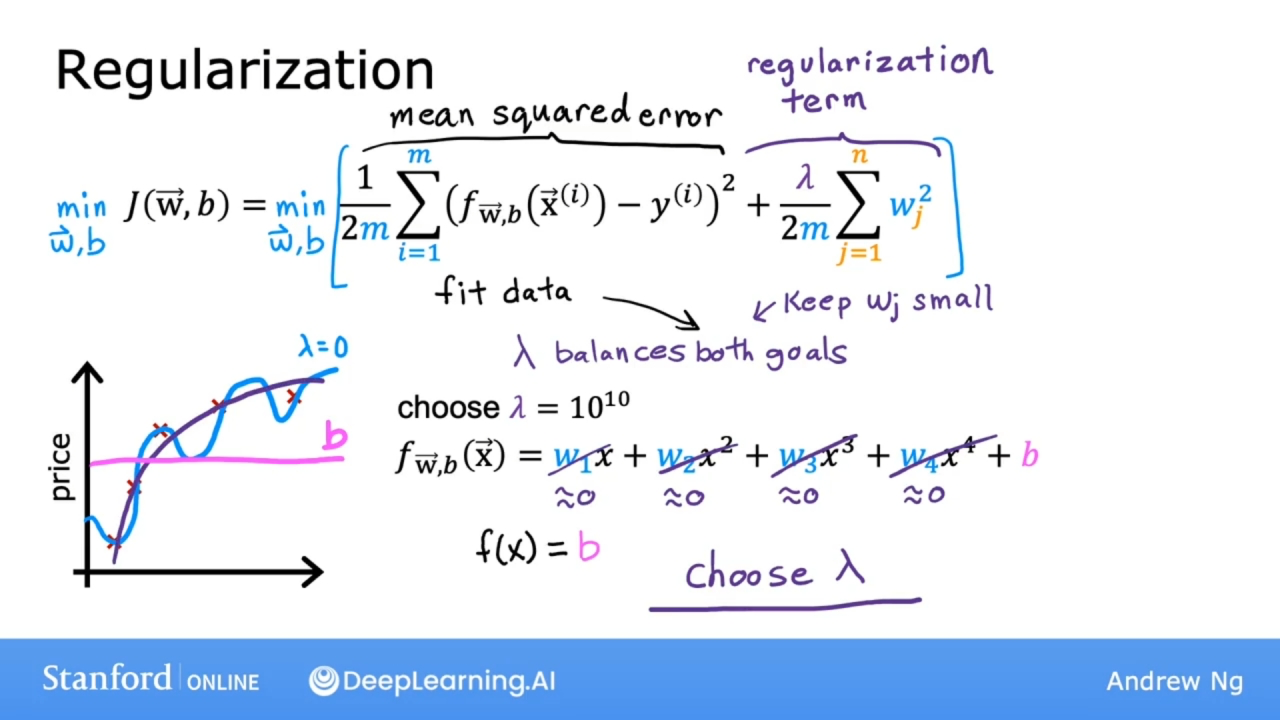
正则化公式
$$J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum\limits_{j=1}^{n} w_j^2$$
其中
$$ f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b \tag{2} $$
参数 $\lambda$ 称为正则化参数
$\frac{1}{2m} \sum\limits_{i = 1}^{m} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2$ 部分称为均方误差成本(mean squared error)
$\frac{\lambda}{2m} \sum\limits_{j=1}^{n} w_j^2$ 部分称为正则化项(regularization term)
正则化项和前面的部分都是按2m的比例缩放, 事实证明, 通过相同的方式缩放两项, 为参数 $\lambda$ 选择一个好的值更容易一些.
特别是, 即使你的训练集规模增加, 使用之前相同的参数 $\lambda$ 现在也更有可能继续工作.
对参数b是否进行正则化, 在实践中几乎没有什么区别.
新的成本函数会权衡下面两个目标:
- 尝试最小化第一项, 会鼓励算法通过最小化预测值和实际值的平方差来很好地拟合训练数据.
- 尽量减少第二项, 算法试图使参数 $w_j$ 保持较小, 这将倾向于减少过度拟合.
如果参数 $\lambda$ 是个非常大的数, 在正则化项上赋予了非常大的权重. 最小化这种情况的唯一方法是确保参数 $w_j$ 的所有值都非常接近0. 此时模型函数f等于参数b, 成为了一条水平直线, 并且欠拟合.
如果参数 $\lambda$ 为0, 则没有正则化项, 则会拟合为过于摇摆, 过于复杂的曲线, 并且会过度拟合.
因此需要一个合适的参数 $\lambda$, 适当地平衡第一项和第二项, 最小化均方误差并保持参数较小.
正则化线性回归

如上图所示公式, 和前面的基本一致, 只是梯度下降时, 参数 $w_j$ 多了 $\frac{\lambda}{m}w_j$ 项.

通过上图的转换, 可得知正则化在每次迭代所做的是将参数 $w_j$ 乘以一个略小于1的数组, 这会缩小参数 $w_j$ 的值.
公式的推导过程, 如下图

正则化逻辑回归
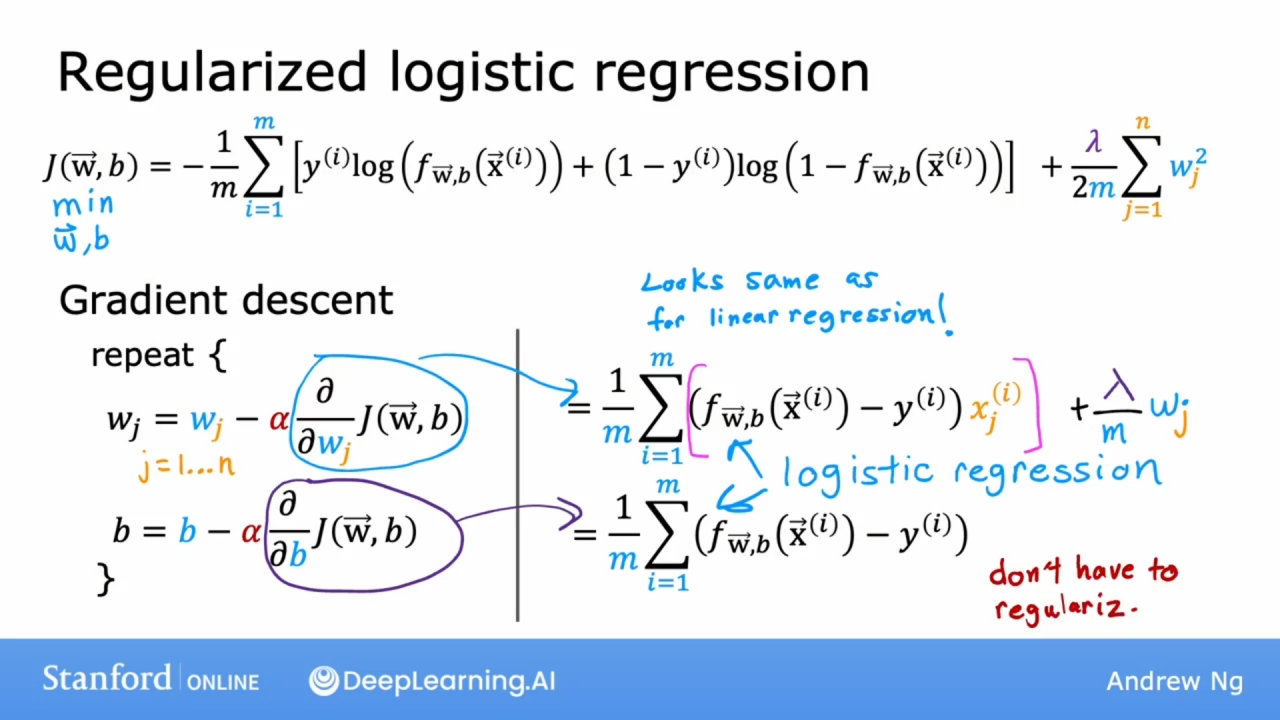
如上图所示公式, 和前面的基本一致, 只是梯度下降时, 参数 $w_j$ 多了 $\frac{\lambda}{m}w_j$ 项. 和线性回归不同的是模型函数 $f_{\mathbf{w},b}$
代码
正规化线性回归
成本函数
def compute_cost_linear_reg(X, y, w, b, lambda_ = 1):
"""
其他参数和以前一样
lambda_是正规化参数
"""
m = X.shape[0]
n = len(w)
cost = 0.0
# 和以前一样
for i in range(m):
f_wb_i = np.dot(X[i], w) + b
cost = cost + (f_wb_i - y[i])2
cost = cost / (2 * m)
# 添加了计算正规化项部分的代码
reg_cost = 0.0
for j in range(n):
reg_cost = reg_cost + w[j]2
reg_cost = (lambda_ / (2 * m)) * reg_cost
# 总成本函数值
total_cost = cost + reg_cost
return total_cost
梯度下降
def compute_gradient_linear_reg(X, y, w, b, lambda_):
m, n = X.shape
dj_dw = np.zeros((n,))
dj_db = 0.0
for i in range(m):
dj_db_i = (np.dot(X[i], w) + b) - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + X[i, j] * dj_db_i
dj_db = dj_db + dj_db_i
dj_dw = dj_dw / m
dj_db = dj_db / m
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_ / m) * w[j]
return dj_dw, dj_db
正规化逻辑回归
成本函数
def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):
m, n = X.shape
cost = 0.0
for i in range(m):
z_i = np.dot(X[i], w) + b
f_wb_i = 1 / (1 + np.exp(-z_i))
# 注意损失函数的前面的负号
cost = cost + -y[i] * np.log(f_wb_i) - (1 - y[i]) * np.log(1 - f_wb_i)
# 最后除以训练集数据数量m
cost = cost / m
reg_cost = 0.0
for j in range(n):
reg_cost = reg_cost + w[j]2
reg_cost = (lambda_ / (2 * m)) * reg_cost
total_cost = cost + reg_cost
return total_cost
梯度下降
def compute_gradient_logistic_reg(X, y, w, b, lambda_):
m, n = X.shape
dj_dw = np.zeros((n,))
dj_db = 0.0
for i in range(m):
z_i = np.dot(X[i], w) + b
f_wb_i = 1 / (1 + np.exp(-z_i))
dj_db_i = f_wb_i - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + X[i, j] * dj_db_i
dj_db = dj_db + dj_db_i
dj_dw = dj_dw / m
dj_db = dj_db / m
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_ / m) * w[j]
return dj_dw, dj_db
