AI-深度学习-第二课

神经网络

Neural Network

历史

起初动机: 通过编程模拟人类大脑, 尝试构建模仿人类大脑的软件.

神经网络的研究始于1950年代, 然后一度失宠.

在1980年代和1990年代初期, 再次流行起来, 并在手写数字识别等一些应用中显示出巨大的吸引力, 这些应用在当时被用于读取邮政编码, 手写支票的美元数字等.

在1990年代后期再度失宠, 大约从2005年开始, 开始复兴, 并通过深度学习重新命名. 从那时起, 神经网络在一个又一个应用领域彻底改变了应用领域.

从语言识别, 到计算机视觉(ImageNet), 到文本或自然语言处理, 到现在神经网络被应用于方方面面.

神经元

Neuron

人类大脑的神经元

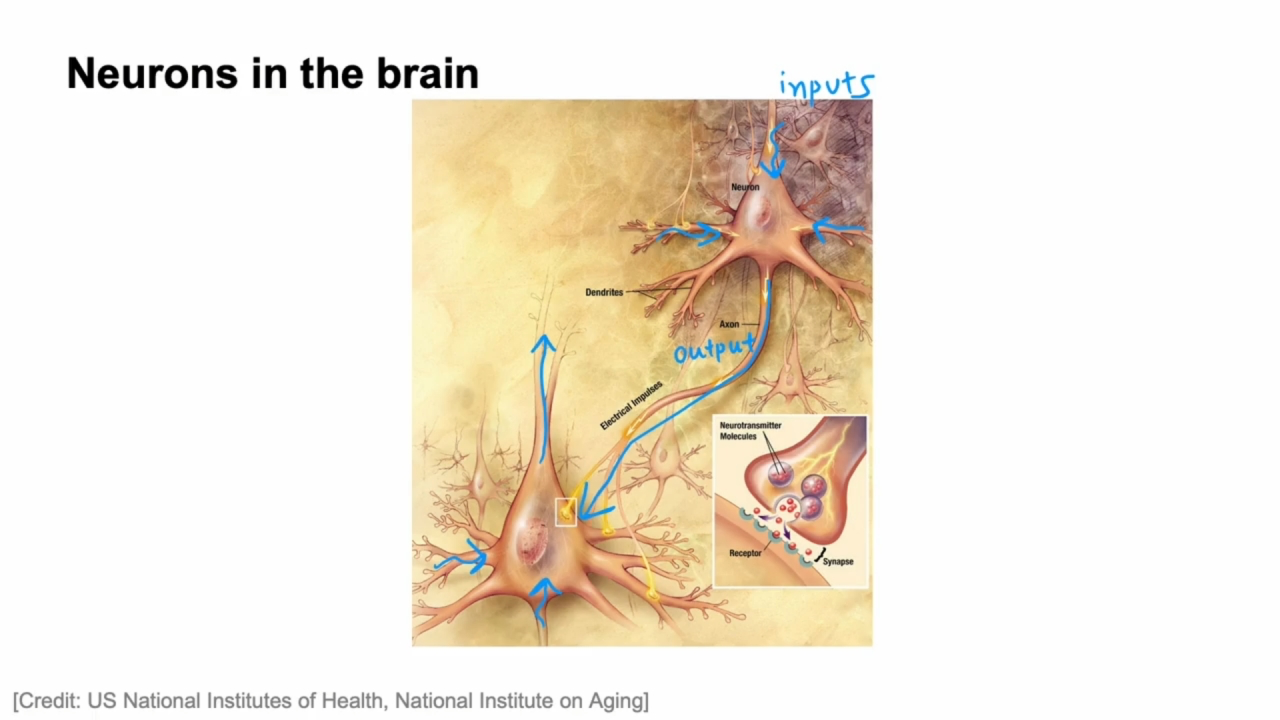
人类的所有思想都来自这样的神经元, 它们发生电脉冲, 有时还会与其他神经元形成新的连接.

神经元有许多输入, 从其他神经元接收电脉冲, 经过计算后, 通过电脉冲发到其他神经元, 上层输出又成为下层输入, 再次聚合来自其他神经元的输入, 然后将自己的输出发到其他神经元.

人工神经元

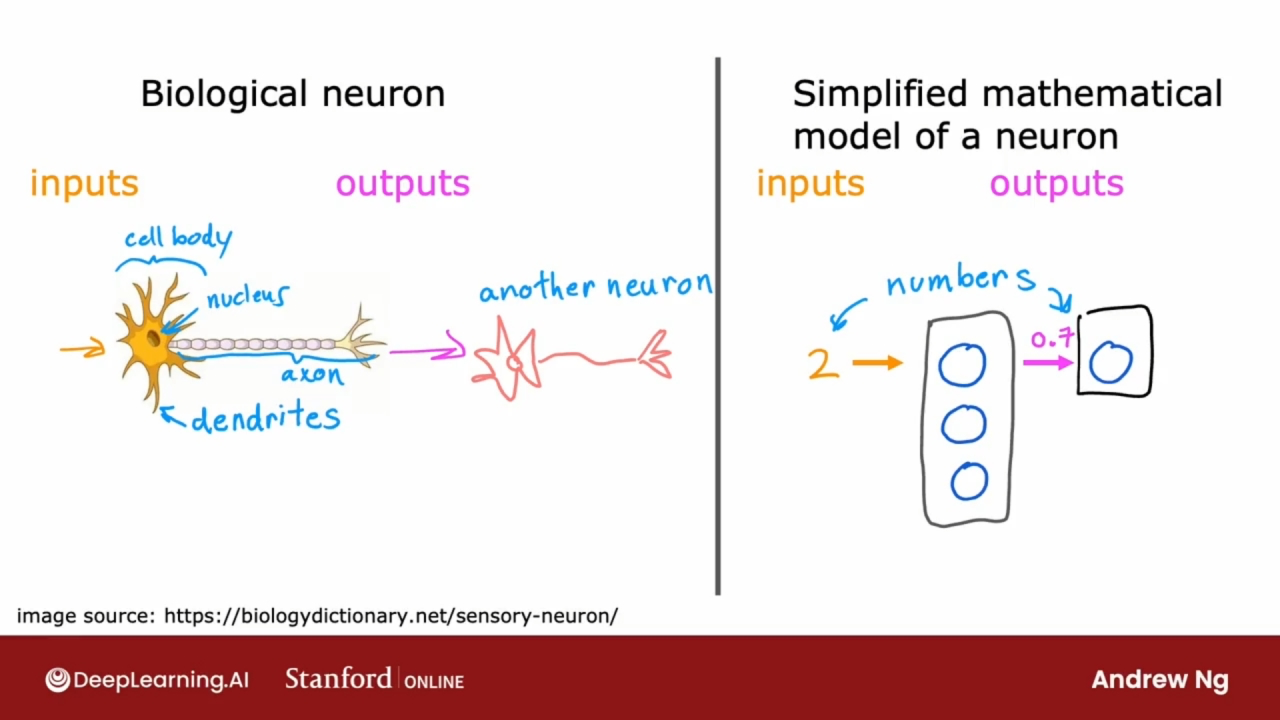
人工神经网络使用了非常简化的生物神经元的数学模型.

上图右边的小圆圈代表神经元, 神经元所做的是, 它接收一些输入(数字), 它进行一些计算并输出一些其他数字, 然后将其作为第二个神经元的输入.

当构建人工神经网络或深度学习算法时, 通常希望同时模拟许多这样的神经元, 这些神经元共同做的是输入一些数字, 进行一些计算, 然后输出一些其他数字.

这只是一个在生物神经元和人工神经元一个松散的类比, 但今天(2023年8月)人类几乎不知道人脑是如何工作的.

事实上, 从事深度学习研究的人已经不怎么关注生物动机了.

为何现在兴起?

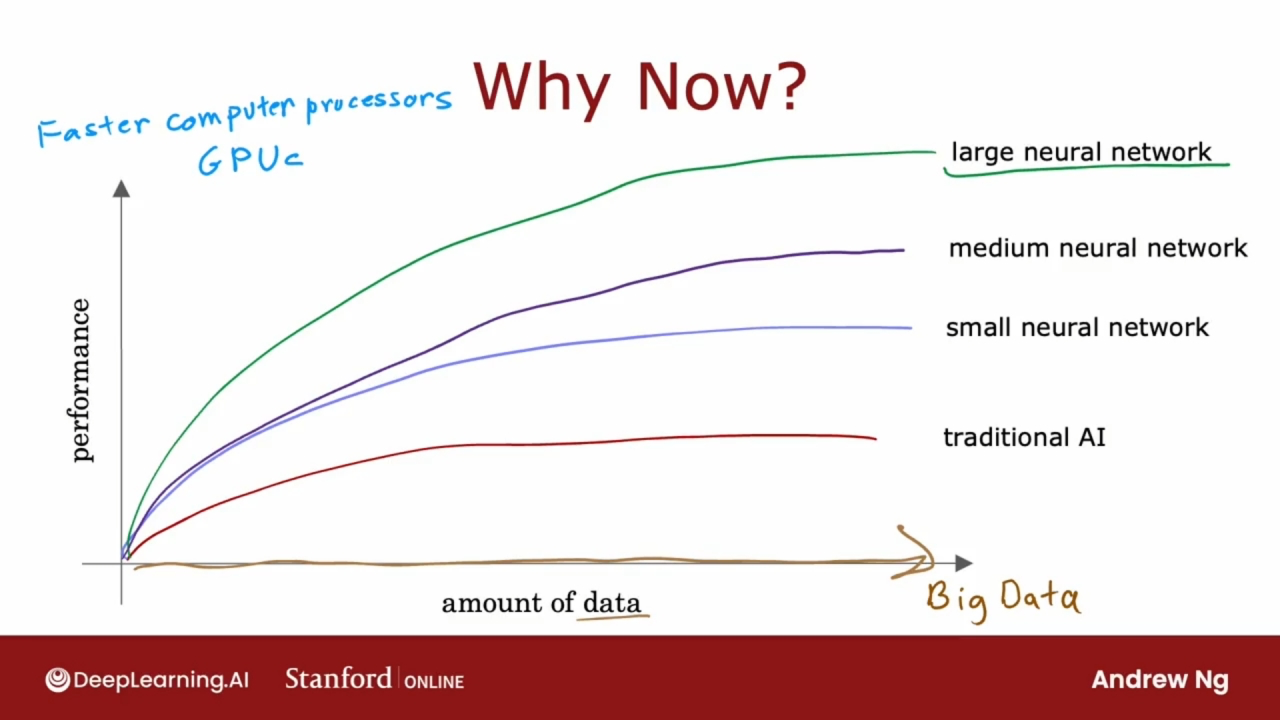
横轴是数据的数量, 纵轴是学习算法的性能.

在过去的几十年里, 随着互联网的兴起, 社会的数字化, 应用程序拥有的数据量稳步向右移动. 在许多应用领域, 数据数量呈爆炸性增长.

传统的机器学习算法, 比如逻辑回归和线性回归, 即使给算法提供更多的数据, 也很难让性能继续上升. 它们无法根据现在提供的数据量进行扩展, 也无法有效利用针对不同应用的数据.

随着训练的神经网络越来越大和复杂, 神经网络的性能越来越高.

对于拥有大量数据(Big Data)的特定应用程序, 如果能够训练非常大的神经网络, 可以在任何事情上获得性能, 这对于传统的学习算法是不可能的.

这导致深度学习算法的起飞.

GPU最初设计用于生成漂亮的计算机图形的硬件, 事实证明对深度学习也非常强大, 这也是让深度学习算法起飞的原因.

工作原理和术语

以下图中预测T恤是否是爆款的例子进行说明

示例中的每个神经元都是一个逻辑回归单元

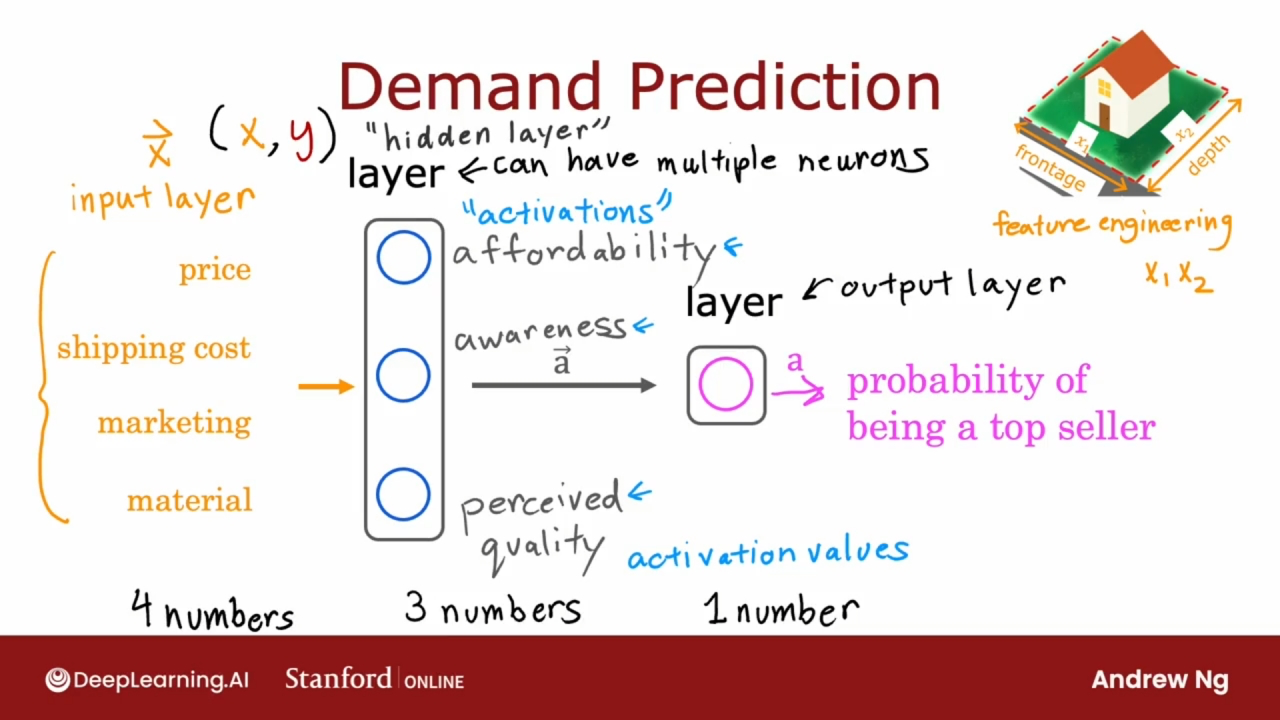
激活(activation): 一个神经元向它下游的神经元发送多少高输出.

层(layer): 是一组神经元, 将相同或相似的特征作为输入, 然后一起输出一些数字.

输入层(input layer): 最初输入到神经网络的数据(矢量x).

输出层(output layer): 最终神经元的输出是神经网络预测的输出.

隐藏层(hidden layer): 神经网络的中间层, 可多个. 在训练集中看不到中间层输出的数据, 因此称为隐藏层.

隐藏层可访问输入层的所有数据, 并设置适当的参数(上一课的正则化)找出单个神经元只关注的功能.

特征矢量x被送到隐藏层, 然后计算激活值, 这些激活值变成另一个矢量a, 该矢量a被送到最终输出层, 最终输出T恤成为畅销商品的概率.

神经网络不需要手动设计特征, 它可以自己学习, 它自己的特征可以使学习问题对自己来说更容易. 这是使神经网络成为当今世界上最强大的学习算法的原因之一.

神经网络好的特性之一是从数据中训练时无需明确决定做什么(隐藏层), 神经网络自行计算出它想在这个隐藏层中使用的特征是什么.

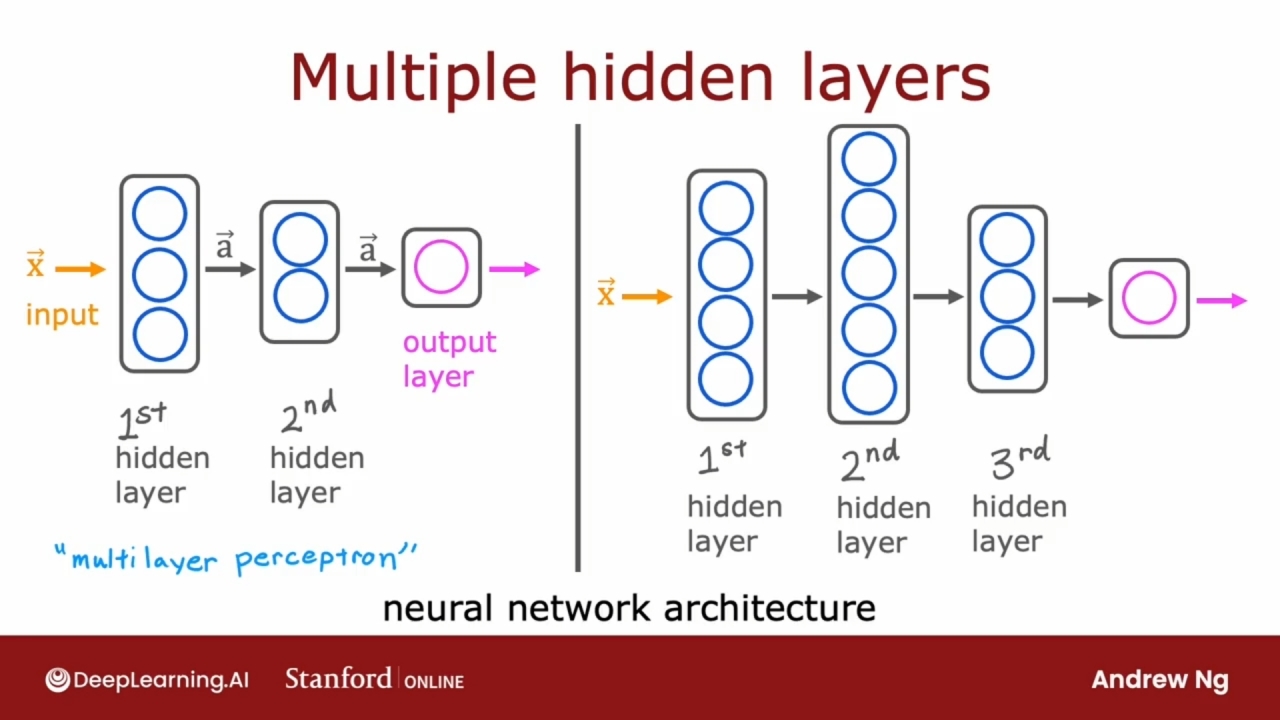
神经网络的隐藏层可以多个, 当构建自己的神经网络时, 需要做出的决定之一是想要多少个隐藏层以及希望每个隐藏层有多少个神经元. 这是神经网络架构(neural network architecture)的问题.

有时这样的多个隐藏层也称为多层感知器(multilayer perception).

选择正确的隐藏层数和每层隐藏单元数会对学习算法的性能产生影响.

应用例子

神经网络在计算机视觉应用中的工作方式

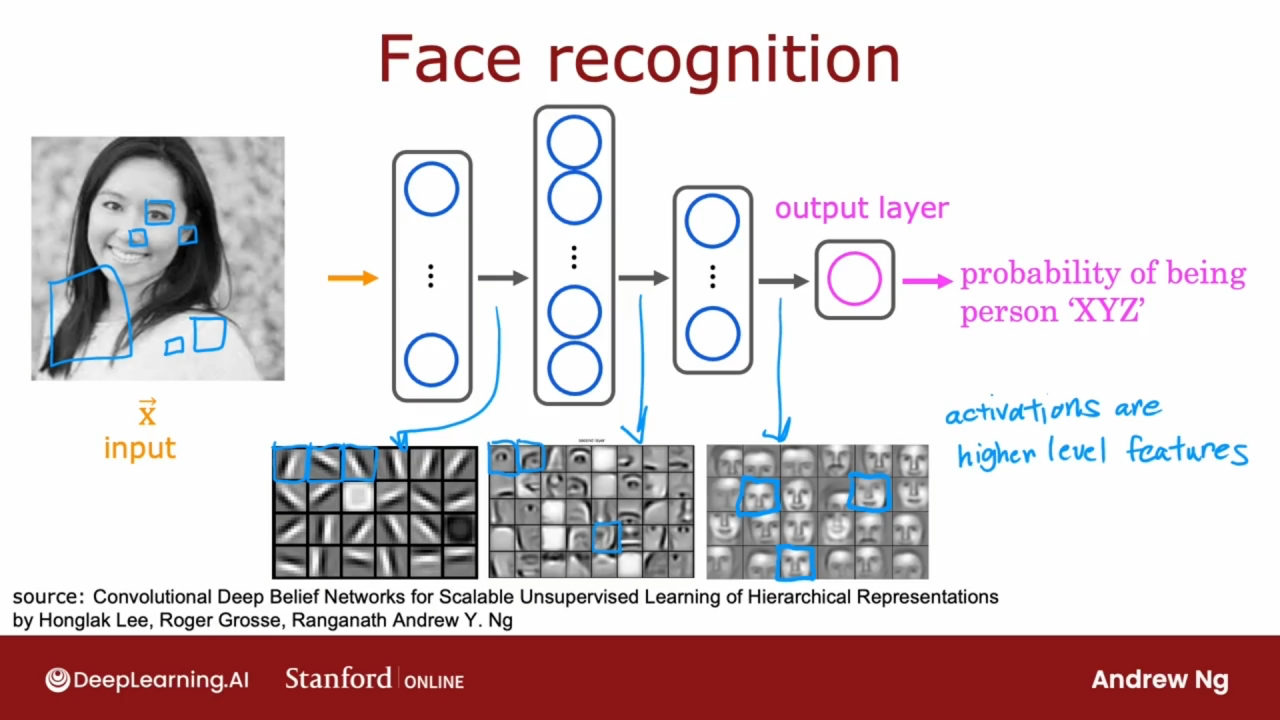
假如图片是1000*1000像素的, 则转换为1百万的像素亮度值的向量作为人脸识别的输入.

人脸识别的问题是能不能训练一个神经网络, 以百万像素亮度值的特征向量为输入, 输出图片中人的身份.

观察人脸识别的隐藏层, 可发现隐藏层中的不同神经元在计算什么:

第一个隐藏层中, 可能会发现神经元正在寻找图像中非常短的线或非常短的边缘.

第二个隐藏层中, 会发现神经元可能会学习将许多小的短线和小的短边段组合在一起, 以寻找面部的各个部分.

最后一个隐藏层中, 会发现神经元会聚合面部的不同部分, 然后尝试检测是否存在更大, 更粗糙的面部形状.

最后, 检测面部与不同面部形状的对应程度可以创建一组丰富的特征, 然后帮助输出层尝试确定人物图片的身份.

神经网络能够自己学习不同隐藏层的特征检测器, 神经网络自己能够从数据中找出特征数据(比如隐藏层的短线, 组合短线, 聚合面部特征等).

第一个隐藏层中的神经元在查看相对较小的窗口以寻找这些边缘. 第二个隐藏层查看较大的窗口, 第三个隐藏层查看更大的窗口. 这些小神经元可视化实际上对应于图像中不同大小的区域.

构建神经网络

工作原理

每一层输入一个数字向量并对其应用一堆逻辑回归单元, 然后计算出另一个数字向量, 然后从一层传递到另一层, 直到到达最终的输出层进行计算(神经网络预测).

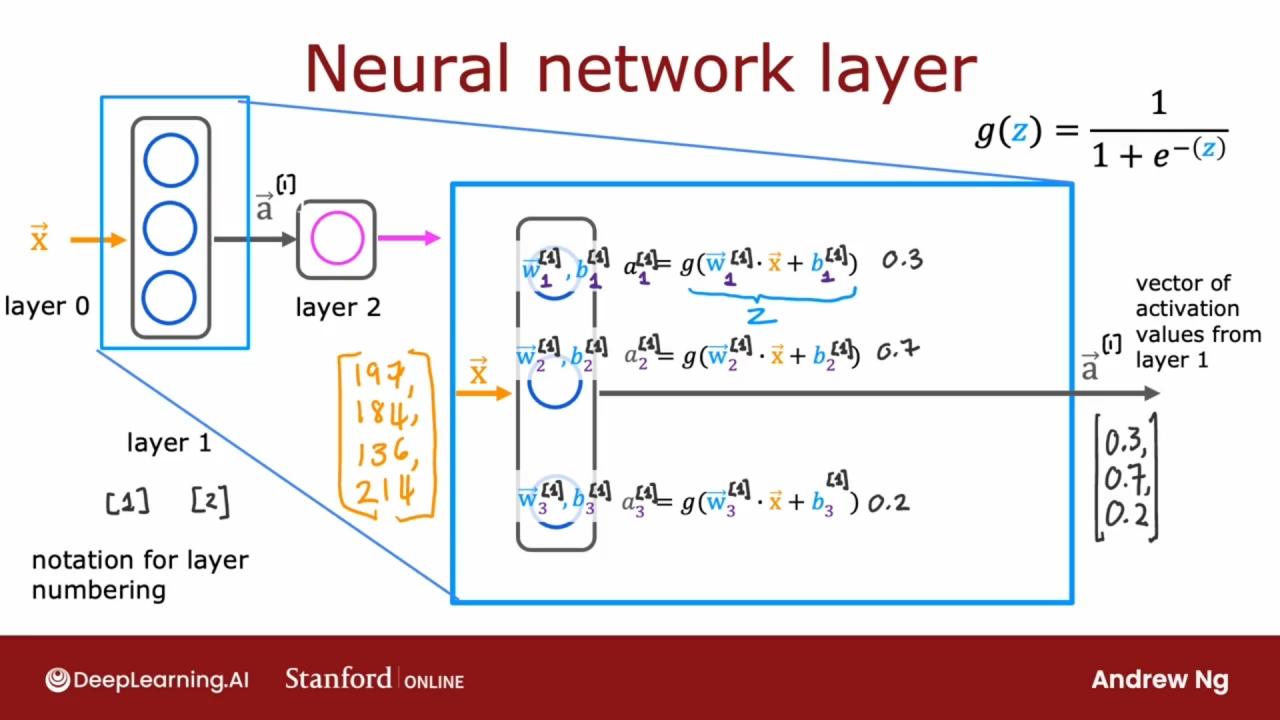
上图是神经网络的第一层(layer 1), 有三个神经元, 每一个都只是在实现一个小逻辑回归单元或小逻辑回归函数.

w, b的下角标数字, 表示在此层的第几个神经元.

w, b, a的上角标数字带有[ ], 表示处在神经网络的第几层, 通常把输入层当作第0层(layer 0).

第一层的神经元输出三个数字, 这三个数字的向量成为激活值向量a.

上图是神经网络的第二层, 第二层的输入是第一层的输出.

这一层是输出层, 只有一个神经元, 输出的是一个数字标量, 而不是数字向量.

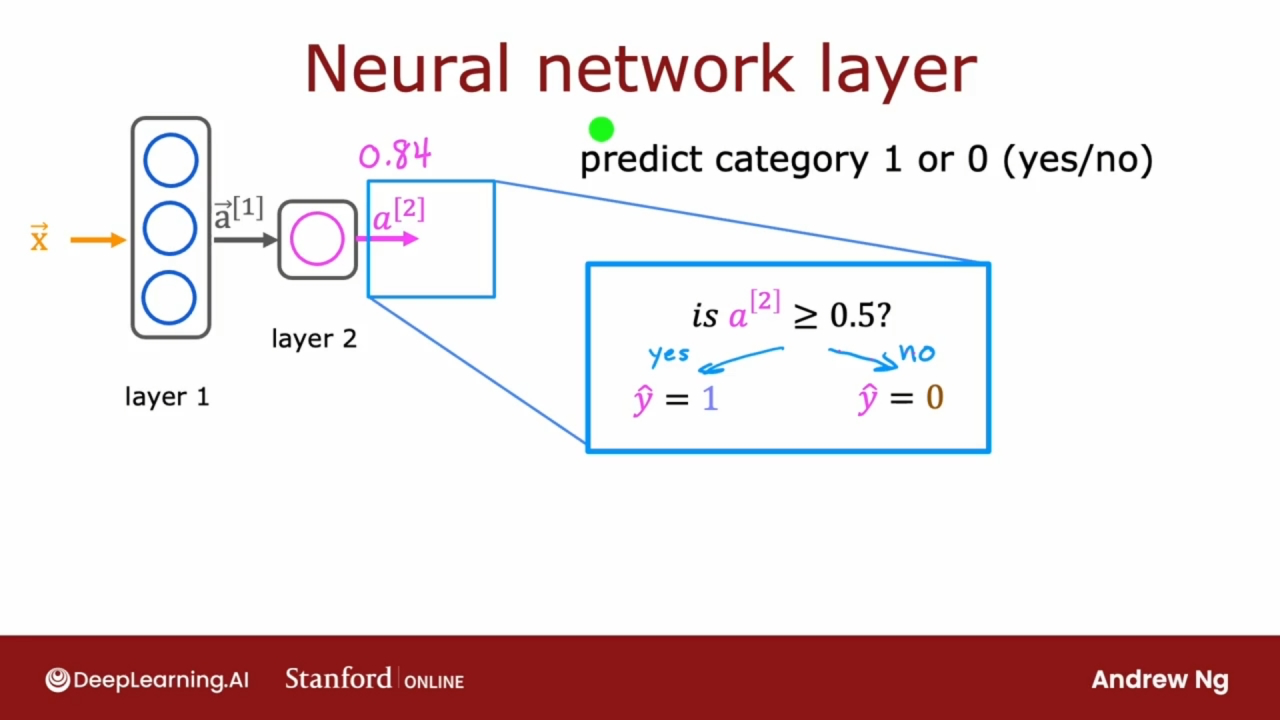
上图是神经网络计算出 $a^{{[2]}}$后, 可以选择执行或不执行最后一个可选步骤.

更复杂的神经网络

下图是一个四层的神经网络, 当说神经网络的层数的时候, 不包括输入层, 但包括输出层.

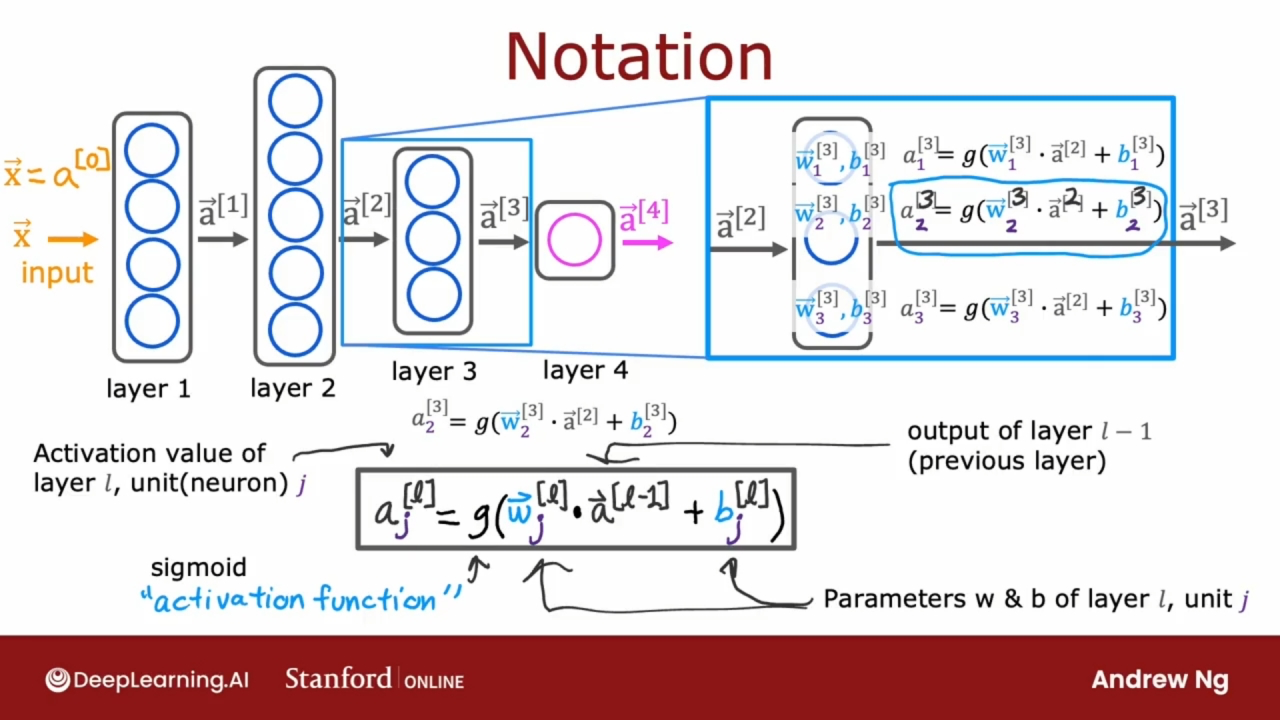
通过上图, 可得到每层单个神经元的计算公式的一般化形式:

$a_j^{{[l]}} = g(w_j^{{[l]}}a^{{[l-1]}} + b_j^{{[l]}})$

其中$l$表示层数, 输入层的向量x可表示为$a^{{[0]}}$.

$a^{{[l-1]}}$表示上一层的输出向量, 也是本层的输入向量.

$g$表示激活函数, 可以是sigmoid函数, 也可以是其他函数.

$j$表示当前$l$层中第$j$个神经元.

前向传播

Forward Propagation

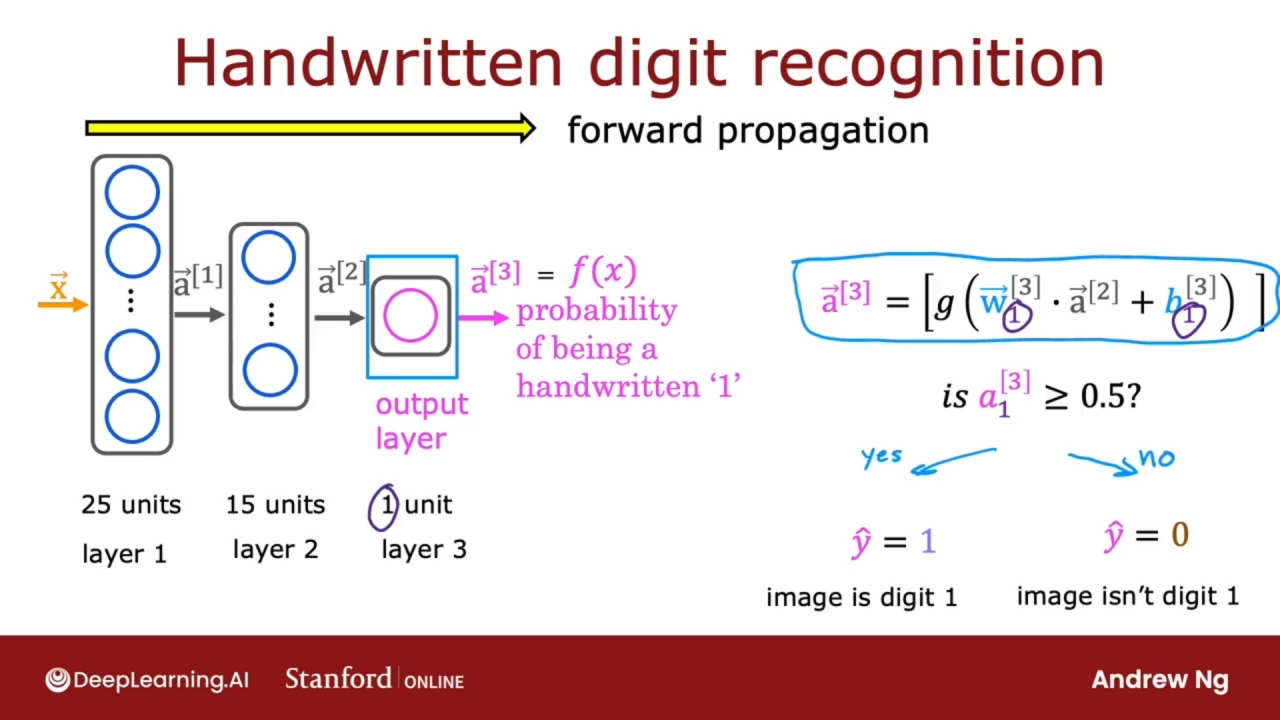
上图是一个前向传播算法的例子, 计算是从左向右进行的, 每层都在传播神经元的激活向量, 与之相对的还有反向传播算法.

前向传播这种类型的神经网络最初有更多的隐藏神经元, 随着离输出层越来越近, 隐藏单元的数量会减少.

TensorFlow框架

TensorFlow是实施深度学习算法的领先框架之一, 另一个是PyTorch.

本课程使用TensorFlow框架.

用法示例

# 输入向量x
x = np.array([[200.0, 17.0]])
# 构建第一层的神经网络
# Dense目前只能暂时使用的密集层(全连接层)
# units是本层使用的神经元数量
# activation是本层神经元使用的激活函数,本例使用sigmoid函数
layer_1 = Dense(units=3, activation='sigmoid')
# 使用x训练神经网络第一层
a1 = layer_1(x)

# 构建第二层的神经网络
layer_2 = Dense(units=1, activation='sigmoid')
# 使用第一层神经网络训练出的数据a1训练神经网络第二层
a2 = layer_2(a1)

# 得到的输出数据a2
# 并根据0.5的阈值进行预测
if a2 >= 0.5:
  yhat = 1
else:
  yhat = 0

表示数据

# 使用双[[目的是创建矩阵
x = np.array([[200.0, 17.0]])

# 2✖️3矩阵,前一个数字表示行数,后一个数字表示列数
x = np.array([
  [1, 2, 3],
  [4, 5, 6]
])
# 只有一行的向量称为行向量
# 只有一列的向量称为列向量

矩阵只是一个二维的数字数组. TensorFlow的惯例是使用矩阵来表示数据.

TensorFlow用于处理非常大的数据集, 并且通过矩阵而不是一维数组表示数据, 能让TensorFlow在内部的计算效率更高.

通过第一层的神经网络计算出的a1是一个1✖️3的矩阵, 通过打印a1, 可得知是一个TensorFlow的数据类型Tensor--张量(为有效地存储和执行矩阵计算而创建的一种数据类型), 且维度是1✖️3, 且里面的数据类型是32位的小数.

可通过a1.numpy()可将a1转换为NumPy数组.

构建神经网络

使用TensorFlow框架构建神经网络代码

# 创建第一层
layer_1 = Dense(units=3, activation='sigmoid')
# 创建第二层
layer_2 = Dense(units=3, activation='sigmoid')
# 使用TensoFlow中的顺序函数,将刚刚创建的两个层顺序串联一起来创建一个神经网络
model = Sequential([layer_1, layer_2])
# 训练数据
× = np.array([
  [200.0, 17.0],
  [120.0, 5.0],
  [425.0, 20.0],
  [212.0, 18.0]
])
# 目标数据
y = np.array([1, 0, 0, 1])

# 编译模型
model.compile(...)
# 拟合数据,在数据集x和目标值y上进行训练
model.fit(x, y)
# 使用新的数据集进行预测
model.predict(x_new)
# 模型预测使用刚刚顺序函数编译的神经网络进行前向传播并为此进行推理

可简化成

# 使用TensoFlow中的顺序函数,将刚刚创建的两个层顺序串联一起来创建一个神经网络
model = Sequential([
  Dense(units=3, activation='sigmoid'),
  Dense(units=1, activation='sigmoid')
])
# 训练数据
× = np.array([...])
# 目标数据
y = np.array([...])

# 编译模型
model.compile(...)
# 拟合数据,在数据集x和目标值y上进行训练
model.fit(x, y)
# 使用新的数据集进行预测
model.predict(x_new)

代码背后

在做什么

上述构建神经网络的代码的背后, TensorFlow框架背后做的事, 如下图

w1_1中的第一个数字表示所在的层数, 第二个数字表示当前层的第几个神经元.

可以看到, 第一层的神经元通过逻辑回归和输入向量x分别输出a1_1, a1_2, a1_3.

a1_1, a1_2, a1_3组成数据a1传入到第二层的单个神经元上进行逻辑回归计算.

自己动手实现

了解TensorFlow框架的底层工作原理很有帮助, 万一出现问题或运行缓慢或出现奇怪的结果或者有bug, 能理解实际发生的事情能使你调试代码更加有效.

# 参数W
W = np.array([
  [1, -3, 5],
  [2, 4, 6]
])
# 参数b
b = np.array([-1, 1, 2])
# 输入数据,即a0,也是x
a_in = np.array([-2, 4])

def dense(a_in, W, b, g):
  """
  a_in是输入的数据,比如x,a1,a2
  W(大写表示矩阵)表示训练的参数w
  b表示训练的参数b
  g是指sigmoid函数
  """
  # 取出当前层的神经元数量
  units = W.shape[1];
  # 创建输出的数据数组,全是0,[0, 0, 0]
  a_out = np.zeros(units)
  # 开始循环遍历,访问是[0, 3)即j的值为0, 1, 2
  for j in range(units):
    # 取出j列的参数w
    w = W[:,j]
    # 计算z值
    z = np.dot(w, a_in) + b[j]
    # 使用sigmoid函数输出结果
    a_out[j] = g(z)
  return a_out

# 下面是调用的伪代码
def sequential(x):
  a1 = dense(x, W1, b1, g)
  a2 = dense(a1, W2, b2, g)
  a3 = dense(a2, W3, b3, g)
  a4 = dense(a3, W4, b4, g)
  f_x = a4
  return f_x

矢量化

原自己使用for循环实现的dense函数, 可使用矢量化高效实现.

神经网络前向传播的矢量化实现代码

# 训练数据X
X = np.array([[200, 17]])
# 参数W
W = np.array([
  [1, -3, 5],
  [2, 4, 6]
])
# 参数B
B = np.array([-1, 1, 2])
# 注意上面的三个变量都是2维数组(矩阵),而不是for循环里一维数组
def dense(A_in, W, B):
  # matmul是NumPy库的矩阵乘法
  Z = np.matmul(A_in, W) + B
  A_out = g(Z)
  # 同时返回的结果也是一个2维数组(矩阵)
  return A_out

矩阵乘法

向量与向量的乘法, 称作点积(Dot Products).

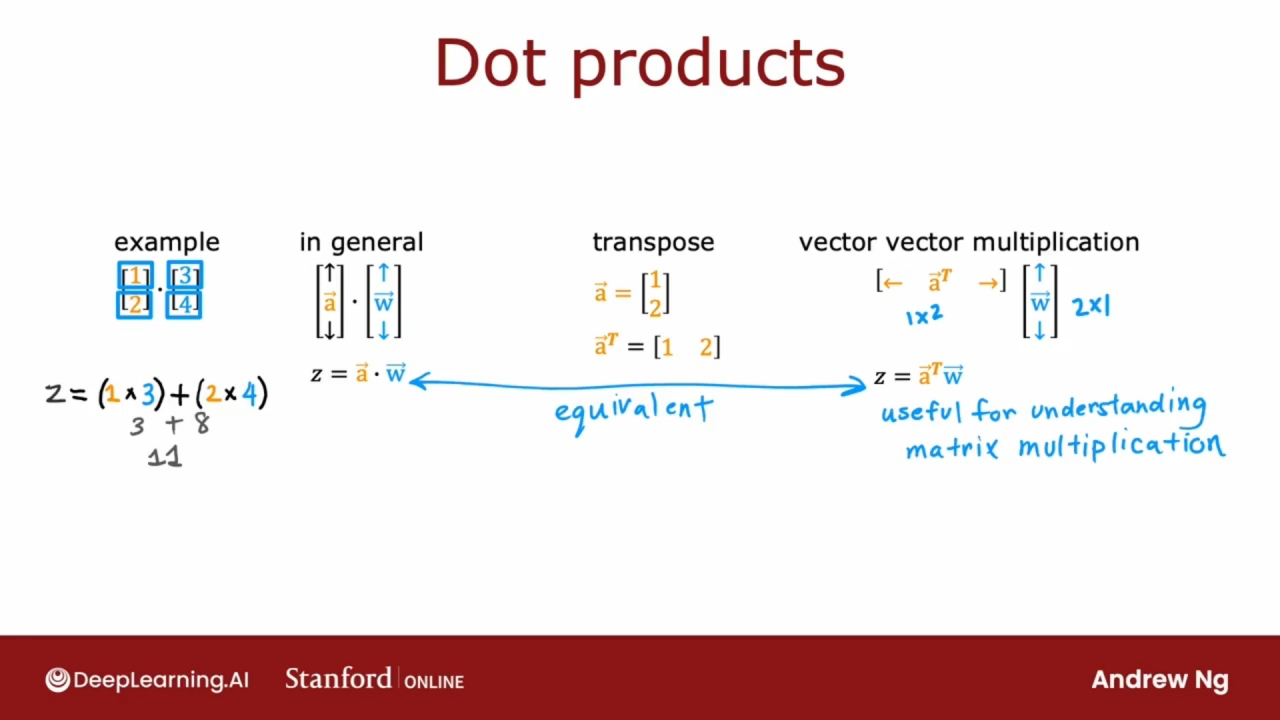
向量与矩阵的乘法

矩阵与矩阵的乘法

转置(transpose)

对向量转置会将此向量从列向量转换为行向量.

转置矩阵的方法是取列, 然后将列放在一行, 一次一列, 最终得到的是转置.

矩阵乘法的一个规则是一个矩阵的列数和另一个矩阵的行数要相等, 因为只能在长度相同的向量之间进行点积.

若有矩阵A是$a \times b$, 矩阵B是$b \times c$, 两矩阵相乘后为矩阵C为$a \times c$.

完整代码

以用法示例中的神经网络为例

# 导库
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from lab_utils_common import dlc
from lab_coffee_utils import load_coffee_data, plt_roast, plt_prob, plt_layer, plt_network, plt_output_unit
import logging

# 导入训练数据,有200个数据
X,Y = load_coffee_data();
# 打印训练数据的数量和有几个特征
print(X.shape, Y.shape)

# 正则化数据
norm_l = tf.keras.layers.Normalization(axis=-1)
norm_l.adapt(X)
Xn = norm_l(X)

# 将数据量增加1000倍
Xt = np.tile(Xn,(1000,1))
Yt= np.tile(Y,(1000,1))   
print(Xt.shape, Yt.shape)

# 设置随机种子,为了得到一致的结果
tf.random.set_seed(1234)
# 创建模型
model = Sequential([
  # 指定输入数据的形状,这允许TensorFlow调整参数w和b的大小
  # 在实际开发中会用model.fit语句代替
  tf.keras.Input(shape=(2,)),
  # 第一层
  Dense(3, activation='sigmoid', name = 'layer1'),
  # 第二层
  Dense(1, activation='sigmoid', name = 'layer2')
])
# 打印模型的一些统计信息,如每层的名称和类型,输出的数据是多少,每层共有多少个参数(包括w和b)
model.summary()
# 获取模型每层的参数数据
W1, b1 = model.get_layer("layer1").get_weights()
W2, b2 = model.get_layer("layer2").get_weights()

# 编译模型
model.compile(
  # 指定损失函数,后面会讲
  loss = tf.keras.losses.BinaryCrossentropy(),
  # 优化器,原本是tf.keras.optimizers.Adam
  # 因为是Mac使用的是M1芯片,所以改成tf.keras.optimizers.legacy.Adam能加快速度
  optimizer = tf.keras.optimizers.legacy.Adam(learning_rate=0.01),
)
# 运行梯度下降,调整参数
model.fit(
    Xt,Yt,            
    epochs=10,
)
# 测试数据,进行预测
X_test = np.array([
    [200,13.9],
    [200,17]
])
# 别忘了要正则化
X_testn = norm_l(X_test)
# 进行预测
predictions = model.predict(X_testn)

# 根据预测的值来判断结果
yhat = np.zeros_like(predictions)
for i in range(len(predictions)):
    if predictions[i] >= 0.5:
        yhat[i] = 1
    else:
        yhat[i] = 0
# 上面的代码可简写为
yhat = (predictions >= 0.5).astype(int)

人工智能

人工智能包括两种截然不同的分支:

• AGI: Artificial General Intelligence 通用人工智能
• ANI: Artificial Narrow Intelligence 狭义人工智能

ANI是只做一件事的AI系统, 一项狭窄的任务, 比如自动驾驶, 网络搜索等等. 近几年, ANI取得了巨大进步, 但不代表着AGI的大量进步.

AGI是可以做任何普通人都可以做的人工智能系统.

如果能模拟很多神经元, 那么就可以模拟人脑或类似人脑的东西, 就会拥有真正的智能系统, 可是事实并非如此简单, 有两个原因:

1. 现在构建的人工神经网络, 非常简单, 逻辑回归单元实际上与任何生物神经元所做的完全不同.
2. 到现在(2023年8月), 我们几乎不知道大脑是如何工作的.

吴恩达老师认为仅仅试图模拟人脑作为通向AGI的途径将是一条极其困难的道路.

有一系列的实验表明大脑的许多不同部分, 仅仅取决于给定的数据(比如图像, 声音等), 好像可能有一个算法只依赖所给的数据, 就能学会相应地处理数据.

一些实验表明人类大脑有惊人的适应性, 具有惊人的可塑性, 意味着能适应任何传感器的输入, 从而学会看, 摸, 听等, 可以复制这个算法并在计算机上实现吗?

在短期内, 即使不追求AGI, 机器学习和神经网络也是非常强大的工具.

TensorFlow细节

下面是用TensorFlow框架实现神经网络的代码

# 导入库
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 创建模型
model = Sequential([
  Dense(units=25, activation='sigmoid'),
  Dense(units=15, activation='sigmoid'),
  Dense(units=1, activation='sigmoid')
])

# 导入loss函数,此次导入的是二元交叉熵损失函数
from tensorflow.keras.losses import BinaryCrossentropy

# 编译模型,并指定损失函数
model.compile(loss=BinaryCrossentropy())

# 训练模型,epochs指定执行梯度下降算法的步骤数
model.fit(X, Y, epochs=100)

代码细节

上图贴出了第一课学习的逻辑回归和本次课程学习的神经网络的对比.

神经网络的代码步骤有以下3步:

1. 创建模型
2. 指定损失函数和成本函数
3. 训练模型以使成本函数最小

如果用神经网络解决线性回归问题(第一课), 使用平方差损失函数, 可如下编码:

from tensorflow.keras.losses import MeanSquaredError
model.compile(loss=MeanSquaredError())

在第三步使用梯度下降训练模型时, TensorFlow使用一种称为反向传播(back propagation)的算法来计算偏导数(后面会讲).

所有的细节部分几乎都由TensorFlow框架完成了.

常用激活函数

Linear activation function 线性激活函数

$g(z) = z$

使用线性激活函数和没有使用激活函数一致, 因此有时也叫没有激活函数.

Sigmoid 函数

$g(z) = \frac{1}{1+e^{-z}}$

用于逻辑回归的激活函数, 取值范围$(0, 1)$

ReLU 函数 Rectified Linear Unit

$g(z) = max(0, z)$

如果$z<0$则取值$0$, 如果$z\ge0$则取值$z$

选择激活函数

输出层

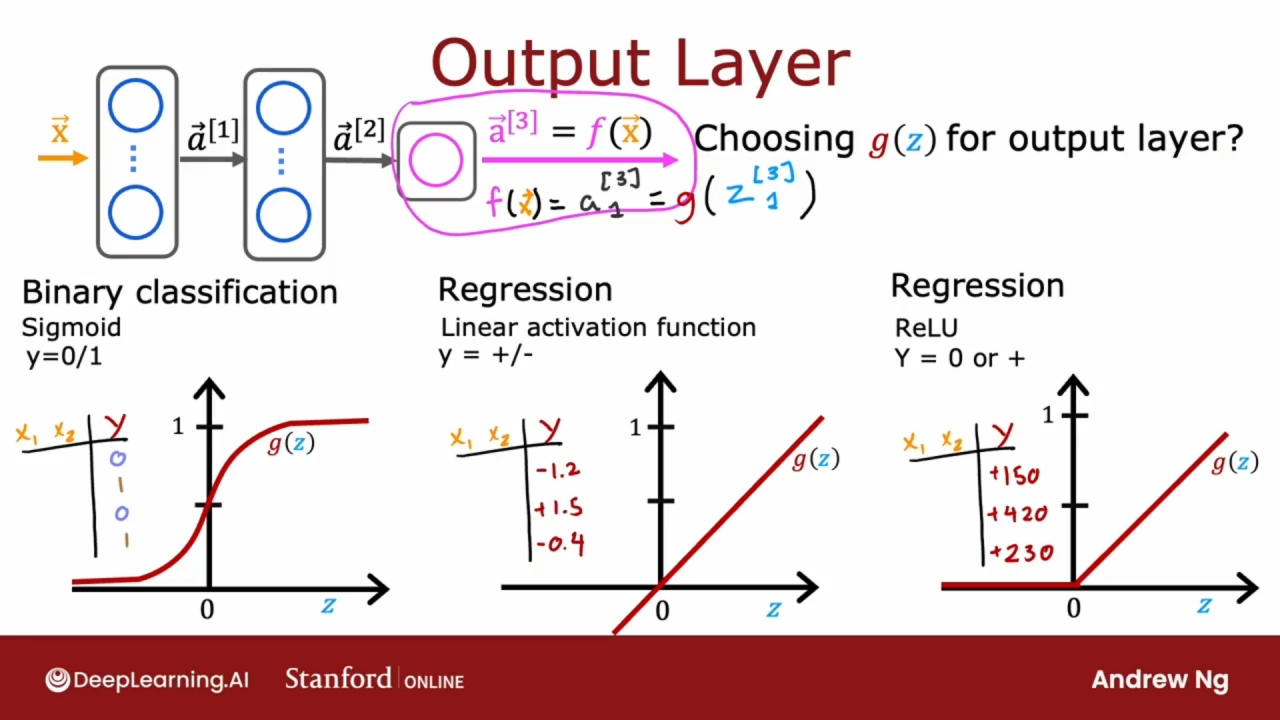
对于输出层, 通常取决于目标数据y是什么样类型的数据.

如果是二元分类问题, y的取值只有0和1, 那选择Sigmoid函数.

当目标数据y是可正可负时, 此时选择线性激活函数.

当目标数据y是非负值时, 此时选择ReLU激活函数.

隐藏层

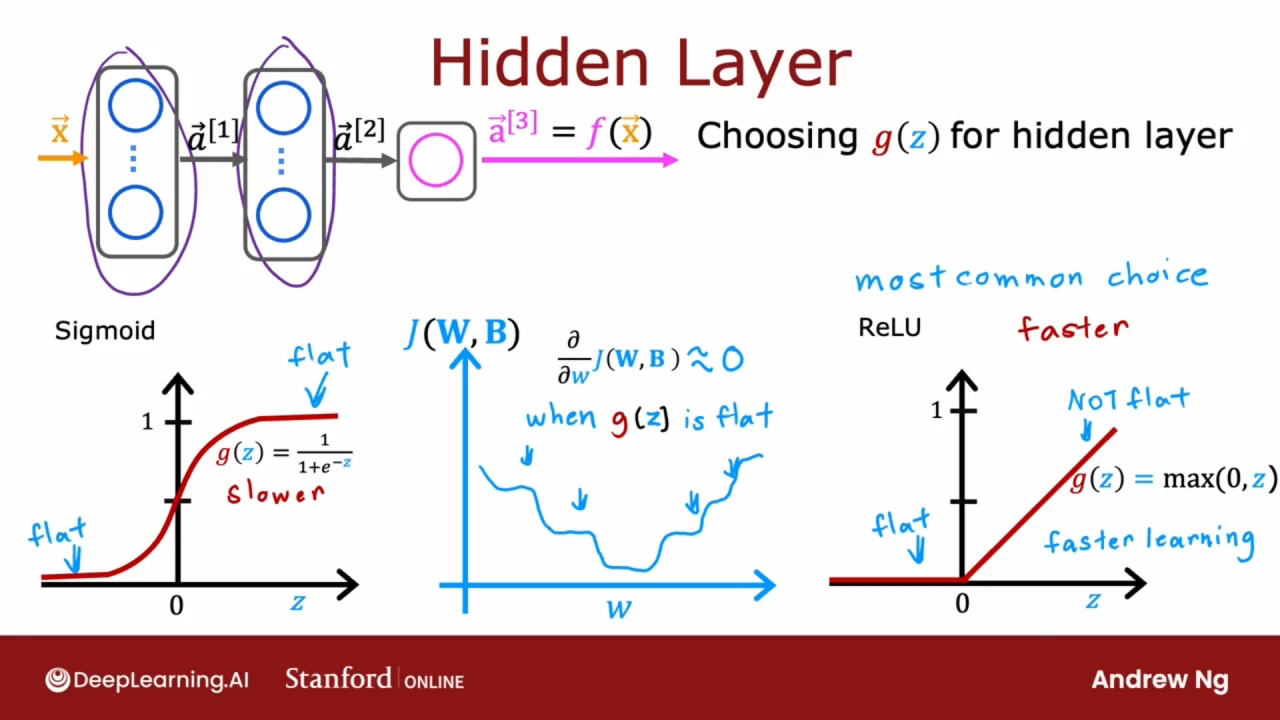
对于隐藏层, 最常用的激活函数是ReLU激活函数.

为什么使用ReLU激活函数:

1. ReLU激活函数比Sigmoid函数计算的更快, 比Sigmoid函数更容易计算.
2. 更重要的是ReLU激活函数只在一侧完全平坦, 而Sigmoid函数在两侧平坦. 当有一个函数在很多地方都平坦时, 梯度下降会很慢, 这会减慢学习速度. ReLU能更快速的梯度下降, 更快的学习.

如何使用

from tensorflow.keras.layers import Dense

# 创建模型
model = Sequential([
  # 使用ReLU激活函数
  Dense(units=25, activation='relu'),
  # 使用线性激活函数
  Dense(units=15, activation='linear')
  # 使用Sigmoid激活函数
  Dense(units=1, activation='sigmoid')
])

虽然还有其他的激活函数, 当ReLU激活函数可以适用当前绝大多数的应用. 其他的激活函数的适用范围较小, 只有小部分案例使之更强.

为何需要激活函数

如果神经网络的所有的神经元都使用线性函数, 整个神经网络将变得与线性回归没什么不同, 这会破坏使用神经网络的全部目的, 因为这样的神经网络无法拟合比线性回归模型更复杂的任何东西.

通过上图一个简单的全是使用线性激活函数神经元的2层神经网络, 经过计算后实际上等价于线性回归.

一般情况下, 如果有个多层神经网络, 对所有的隐藏层使用线性激活函数, 并对输出层使用线性激活函数, 那么模型的计算完全等同于线性回归的输出.

如果对所有的隐藏层使用线性激活函数, 并对输出层使用Sigmoid激活函数, 那么此模型等同于逻辑回归模型.

上述是神经网络为何需要激活函数, 但不仅仅到处都是线性激活函数的原因.

多分类问题

定义

多分类(Multiclass)问题是指分类问题有两个以上可能的输出标签, 而不仅仅是0或1.

多分类问题仍然是一个分类问题, 因为标签y只能取少量的离散类别而不是任何数字, y可以取两个以上的可能值.

如上图的右边所示的一个4分类问题.

Softmax回归

推广

逻辑回归(2个可能输出)推广到Softmax回归(4个可能输出)

如上图所示推到过程

2个可能结果(y=1,0)的逻辑回归公式:

$a_1 = g(z) = \frac{1}{1+e^{-z}} = P(y=1|X)$

$a_2 = 1 - a_1 = P(y=0|X)$

4个可能结果(y=1,2,3,4)的Softmax回归公式:

$a_1 = \frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}+e^{z_4}} = P(y=1|X)$

$a_2 = \frac{e^{z_2}}{e^{z_1}+e^{z_2}+e^{z_3}+e^{z_4}} = P(y=2|X)$

$a_3 = \frac{e^{z_3}}{e^{z_1}+e^{z_2}+e^{z_3}+e^{z_4}} = P(y=3|X)$

$a_4 = \frac{e^{z_4}}{e^{z_1}+e^{z_2}+e^{z_3}+e^{z_4}} = P(y=4|X)$

其中 $a_1 + a_2 + a_3 + a_4 = 1$

推广到更一般的情况, y的取值从1到N, 使用变量j代表y其中的一个取值

$a_j = \frac{e^{z_j}}{\sum_{k=1}^{N} e^{z_k}} = P(y=j|X)$

同样有: $\sum_{k=1}^{N}a_k = 1$

损失函数和成本函数

逻辑回归的损失函数:

$loss = -y \log{a_1} - (1 - y)\log{(1-a_1)}$

可知当$y=1$时 $loss = -\log{a_1}$

当$y=0$时 $loss = -\log{a_2}$

逻辑回归的成本函数:

$J(\mathbf{w},b) = \frac{1}{m} \sum_{i=1}^{m}loss$

推广到Softmax回归, 则有

当$y=0$时 $loss(a_j) = -\log{a_j}$

此函数的图像如课件图片所示, 如果 $a_j$ 非常接近1, 损失就会很小, $a_j$ 越小, 损失越大, 这会让激励算法使 $a_j$ 尽可能大, 尽可能接近1. 无论y的实际值是多少, 您都希望算法让y成为该值的可能性非常大.

在这个损失函数中, 每个训练示例中的y只能取一个值$j$, 最终只针对 $a_j$ 的一个值计算 $a_j$ 的负对数(损失函数), 不会计算其他的y不是$j$的损失函数.

代码实现

将输出层变为有10个可能值的Softmax输出层, 如下图所示

说明(只是说明)代码

import tensorflow as tf
from tensorflow.keras import Sequential 
from tensorflow.keras.layers import Dense
# 创建模型
model = Sequential([
  Dense(units=25, activation='relu'),
  Dense (units=15, activation='relu'),
  # 输出层的激活函数换成softmax函数
  Dense (units=10, activation='softmax')
)]
# 导入训练此模型使用的损失函数
from tensorflow.keras.losses import SparseCategoricalCrossentropy
# 编译模型,使用导入的损失函数
# SparseCategoricalCrossentropy是指仍然将y分类(有CategoricalCrossentropy后缀),而Sparse(稀疏)是指y只能取这10个值之一
# Sparse(稀疏)是指每个取值的数字都是这些类别之一
model.compile(loss=SparseCategoricalCrossentropy())

注意: 请不要在实际开发中使用上述代码, 因为会有更高效的实现.

更优实现

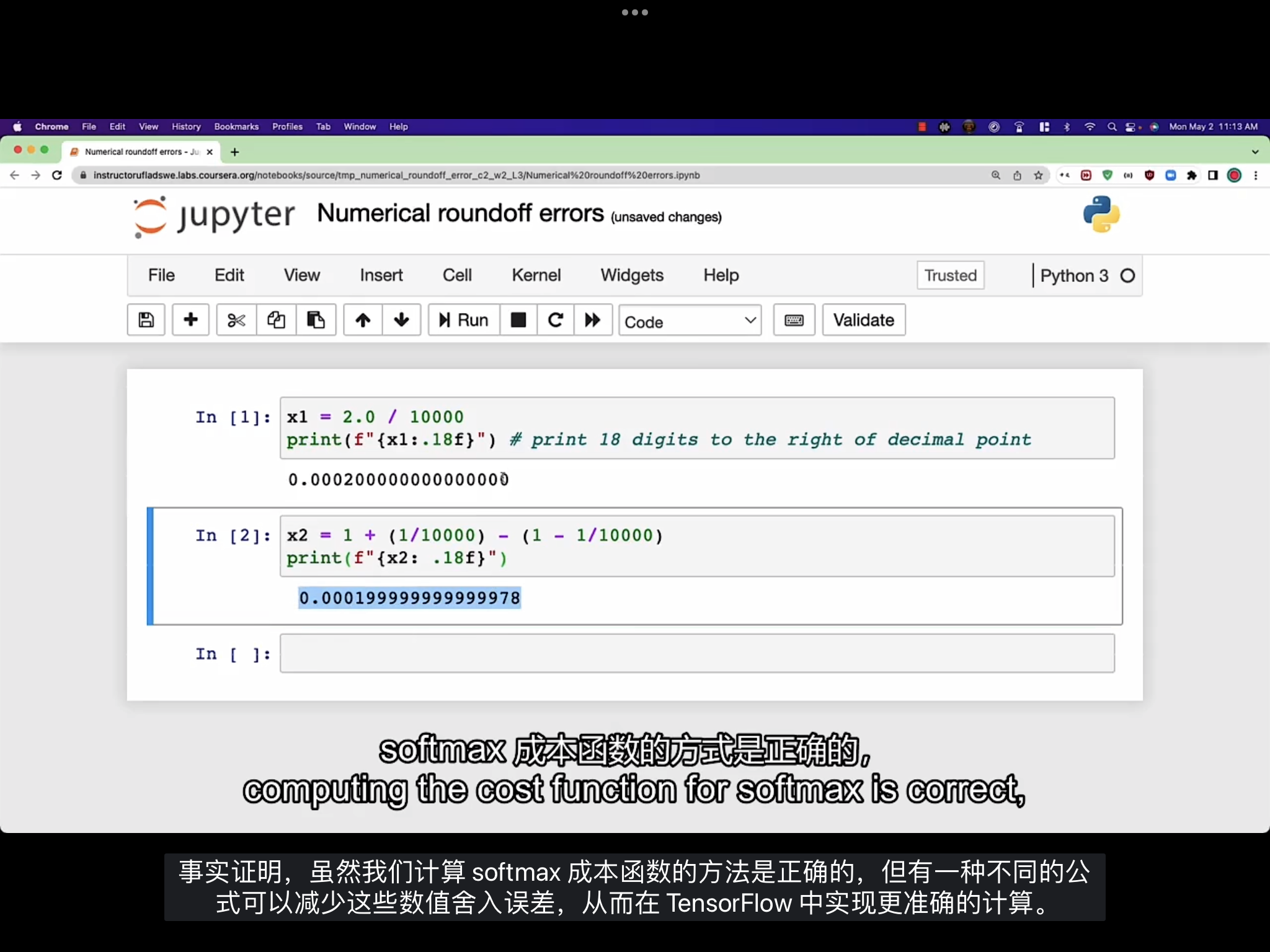
如上图所示, 虽然在数学上两个式子相等, 但计算机计算出的结果却不一致(精度损失).

因此要选择更好的计算方式.

虽然原来计算Softmax成本函数的方法是正确的, 但有一种不同的方式可以减少这些数值舍入误差, 从而在TensorFlow中实现更准确的计算.

逻辑回归

对于逻辑回归, 通常数值舍入的误差还不错.

如果允许TensorFlow不必计算a作为中间项, 并扩展为图上所示更精确的表达式. TensorFlow可以重新排列这个表达式中的项, 并提出一种在数值上更准确的方法来计算这个损失函数.

更优的实现代码是

# 创建模型
model = Sequential([
  Dense(units=25, activation='relu'),
  Dense (units=15, activation='relu'),
  # 输出层的激活函数换成线性激活函数
  Dense (units=10, activation='linear')
)]
# 添加参数from_logits=True
model.compile(loss=BinaryCrossentropy(from_logits=True))

logits 基本上是指数字 $z$, TensorFlow会将 $z$ 计算为中间值, 但它可以重新排列项以使其计算更准确.

重要的代码细节

已经将神经网络的输出层改为线性激活函数了, 而不再是Softmax函数, 神经网络的最后一层不再输出概率值, 而是 $z$ 值. 因此在进行实际的预测时, 按照下面方式更改代码

# 训练模型
model.fit(X, Y, epochs=100)
# 训练模型之后,用旧的训练集检验预测结果
logit = model(X)
# 进行预测,注意逻辑回归使用的是sigmoid
f_x = tf.nn.sigmoid(logit)

Softmax回归

涉及到Softmax回归时, 数值舍入的误差会变得更糟糕.

如上图的公式所示, 如果 $z$ 中的一个值很小或很大, 会造成 $e^z$ 的值跟着大和小. 通过重新排列项, TensorFlow可以避免其中一些非常小或非常大的数字.

更优的实现代码是

# 创建模型
model = Sequential([
  Dense(units=25, activation='relu'),
  Dense (units=15, activation='relu'),
  # 输出层的激活函数换成线性激活函数
  Dense (units=10, activation='linear')
)]
# 导入训练此模型使用的损失函数
from tensorflow.keras.losses import SparseCategoricalCrossentropy
# 编译模型,使用导入的损失函数,添加参数from_logits=True
model.compile(loss=SparseCategoricalCrossentropy(from_logits=True))

和原来的实现代码做的是几乎相同的事情, 更优的实现在数字上更准确.

重要的代码细节

已经将神经网络的输出层改为线性激活函数了, 而不再是Softmax函数, 神经网络的最后一层不再输出概率值, 而是 $z$ 值. 因此在进行实际的预测时, 按照下面方式更改代码

# 训练模型
model.fit(X, Y, epochs=100)
# 训练模型之后,用旧的训练集检验预测结果
logits = model(X)
# 进行预测,注意Softmax回归使用的是softmax
f_x = tf.nn.softmax(logits)

多标签分类

多标签分类问题示例

因为与单个输入相关联的图像是三个不同的标签, 对应于图像中是否有汽车, 公共汽车或行人. 这种情况下, y的目标实际上是三个数字的向量, 这与多分类不同. 多分类的y是一个数字, 但该数字可以有多个不同的可能值.

如何构建用于多标签分类的神经网络?

一种笨方法是使用三个独立的神经网络分别判断是否有汽车, 公共汽车和行人.

但还有另一种方法可以做到这一点, 就是训练一个神经网络可同时检测汽车, 公共汽车和行人这三者. 一个神经网络解决三个二元分类问题, 可以对输出层的三个神经元节点中的每一个使用Sigmoid激活函数, 如下图

多分类问题和多标签分类有时会相互混淆, 需要进行区分.

高级优化

Adam算法

在梯度下降算法中, 如果学习率$\alpha$设置的较小, 到达成本最小化的点需要较多的迭代步数, 能不能有一个算法可自动增加学习率$\alpha$, 让它采取更大的步骤并更快地达到最小值?

如果学习率$\alpha$设置的较大, 梯度下降会来回摆动, 能不能有一种算法可自动降低学习率$\alpha$, 可让它采取更平滑的路径到达最小值?

Adam(Adaptive Moment estimation) 算法可做到这一点.

Adam算法没有使用单一的全局学习率$\alpha$, 它对模型的每个参数使用不同的学习率.

Adam算法的直觉是:

1. 如果参数w和b似乎继续沿着大致相同的方向移动, 应该增加该参数的学习率$\alpha$.
2. 如果参数w和b不断来回震荡, 为了不让参数来回摆动或弹跳, 应该稍微减少钙参数的学习率$\alpha$.

代码示例

# 创建模型
model = Sequential([
  Dense(units=25, activation='relu'),
  Dense (units=15, activation='relu'),
  # 输出层的激活函数换成线性激活函数
  Dense (units=10, activation='linear')
)]
# 导入训练此模型使用的损失函数
from tensorflow.keras.losses import SparseCategoricalCrossentropy
# 导入训练此模型的优化器Adam
from tensorflow.keras.optimizers import Adam
# 编译模型,使用Adam优化器,默认学习率0.001
# 使用导入的损失函数,添加参数from_logits=True
model.compile(optimizer=Adam(learning_rate=1e-3),
  loss=SparseCategoricalCrossentropy(from_logits=True))
# 训练模型
model.fit(X,Y,epochs=100)

卷积神经网络

卷积层

密集层(Dense Layer): 每个神经元的输出是前一层的所有激活输出的函数.

Each neuron output is a function of all the activation outputs of the previous layer.

卷积层(Convolutional Layer): 每个神经元只查看前一层的部分输入.

Each Neuron only looks at part of the previous layer's inputs.

为何要如此做:

1. 使用卷积层加快了计算速度.
2. 使用卷积层需要更少的训练数据, 并且也不太容易过度拟合.

下图是个手写数字识别的卷积层的说明

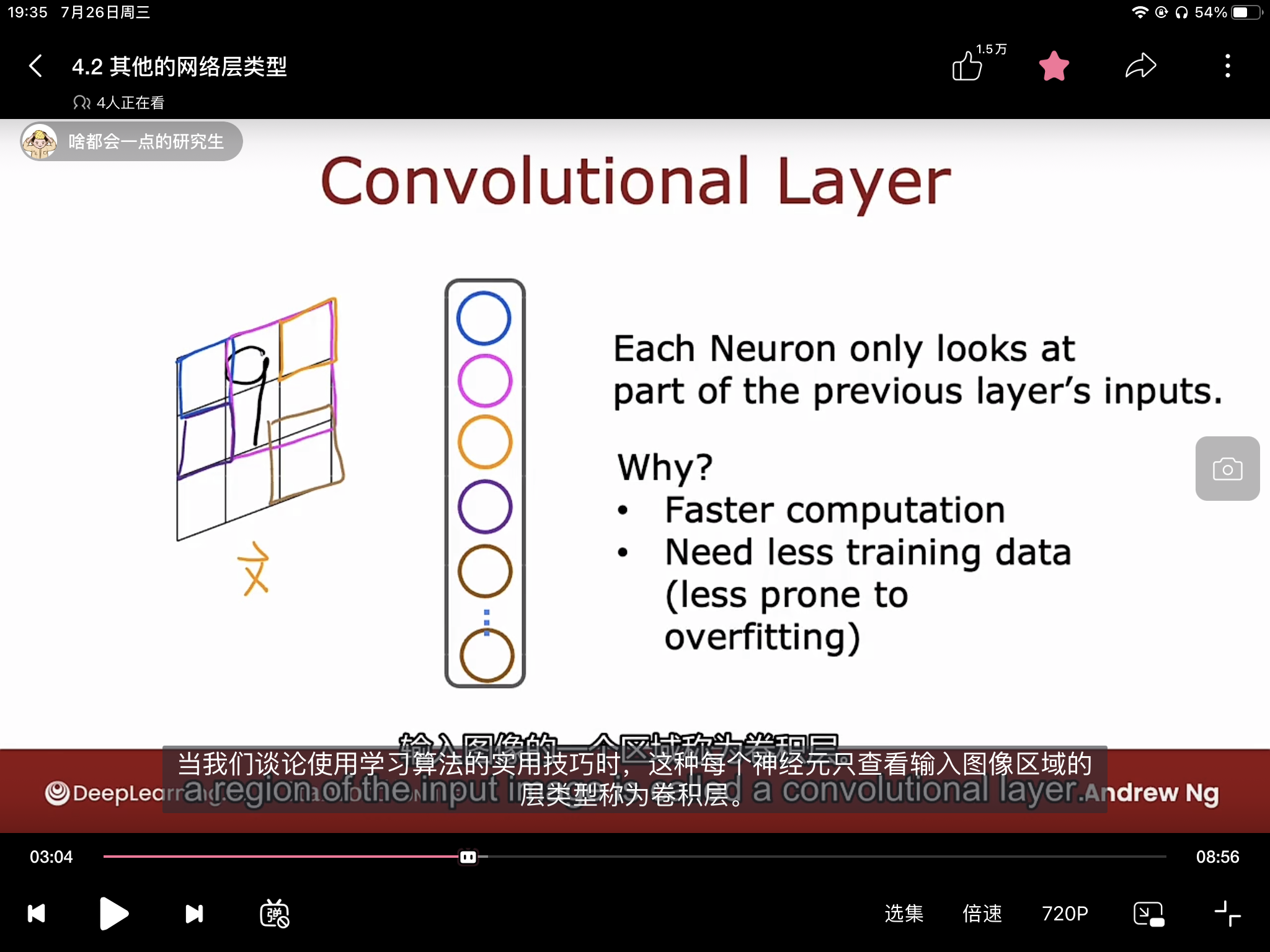
该层的单个神经元只查看部分图像区域.

卷积神经网络

如果神经网络有多个卷积层, 有时该神经网络称为卷积神经网络(Convolutional Neural Network).

下图是个心电图(EKG)预测心脏病的神经网络示例

第一层的神经元只查看部分的心电图数据, 第二层的神经元只查看部分第一层的输出.

对于卷积层, 有很多架构选择, 如单个神经元查看的输入窗口大小, 每层的神经元个数, 通过有效地选择这些架构参数, 可以构建新版本的神经网络, 对于某些应用程序来说, 甚至比密集层更有效.

计算图

Computation Graph

计算图是深度学习的一个关键概念, 也是TensorFlow等编程框架如何自动计算神经网络的导数的算法.

构建计算图

如下图构建一个简单的计算图

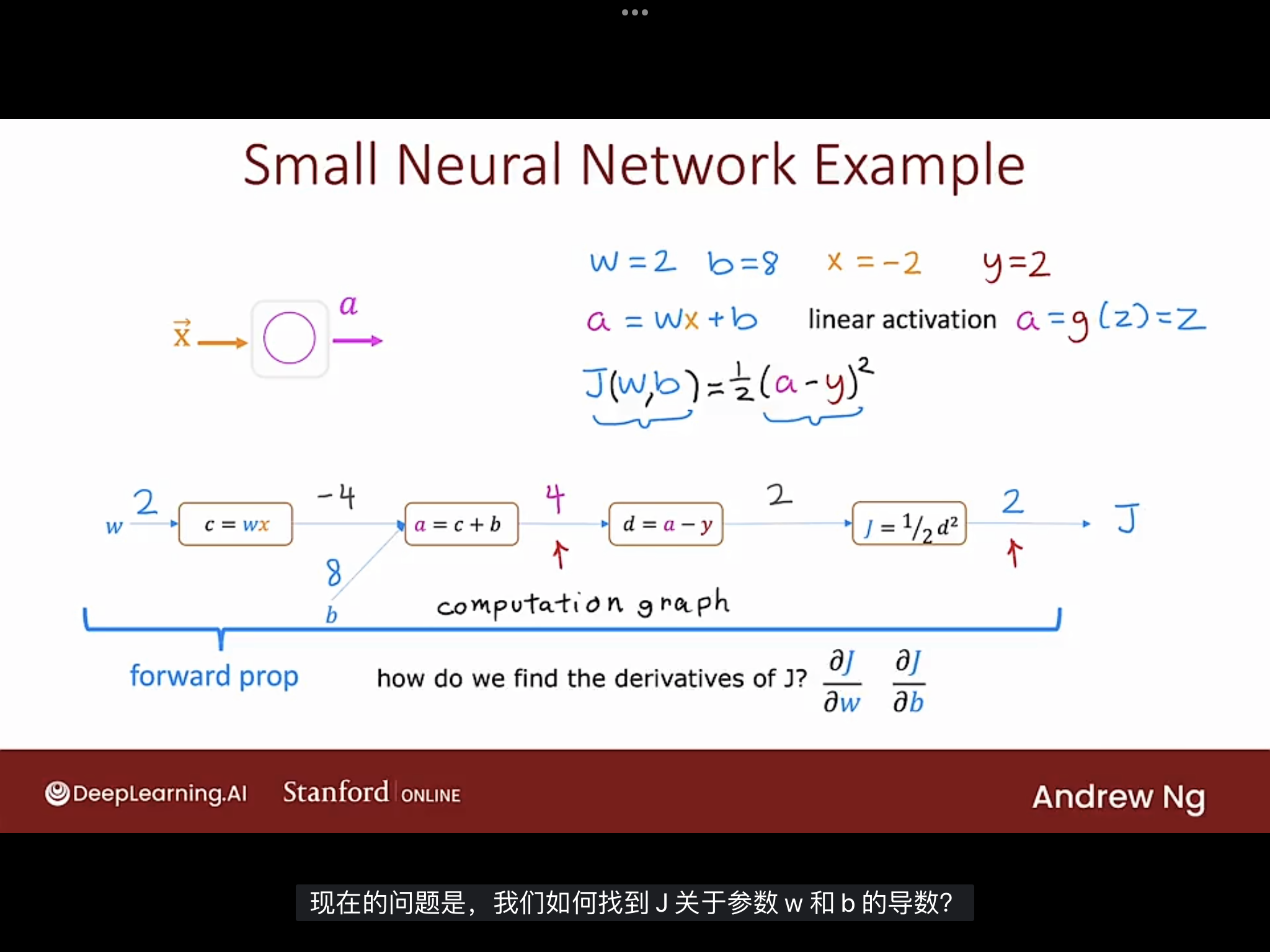
将计算成本函数的步骤分解成更小的步骤, 构建出计算图.

图片的计算图显示了如何计算神经网络输出a的前向传播(forward prop)步骤.

计算导数

下图显示了如何计算导数$\frac{\partial J}{\partial w}$和$\frac{\partial J}{\partial b}$

计算导数是一个从右到左的计算, 称为反向传播(back prop).

首先计算出$j$和$d$的导数$\frac{\partial J}{\partial d} = 2$

然后向左计算$j$和$a$的导数$\frac{\partial J}{\partial a} = 2$

在计算过程中使用了导数的链式法则: $\frac{\partial J}{\partial a} = \frac{\partial d}{\partial a} \times \frac{\partial J}{\partial d}$

一直向左, 直到计算出$j$和$w$的导数$\frac{\partial J}{\partial w} = -4$, $j$和$b$的导数$\frac{\partial J}{\partial b} = 2$

反向传播是计算导数的有效方法, 因为如果需要知道$j$和$w$的导数$\frac{\partial J}{\partial w}$, 就要先计算$j$和$c$的导数$\frac{\partial J}{\partial c}$, 依次类推. 所以通过一次的从右向左计算, 就可以找到$j$与中间量, $j$与参数$w, b$的导数.

反向传播高效的原因, 如果一个神经网络有$n$个节点, $p$个参数, 反向传播允许使用大约$n+p$步, 而不是 $n \times p$步(前向传播的计算步数)计算$j$与参数$w, b$并的导数.

有效构建机器学习

使机器学习系统运行良好且有效率, 在很大程度上取决于您在机器学习项目过程中做出下一步该做什么的正确决策的能力.

机器学习诊断

Machine Learning Diagnostic

如果在训练模型过程中, 发现模型在预测中出现了无法接受的重大错误, 那接下来该做什么?

1. 获取更多的训练数据
2. 尝试更小的特征集
3. 尝试增加额外的特征
4. 尝试增加多项式特征
5. 尝试减少正则化参数
6. 尝试增加正则化参数

在给定的机器学习应用程序中, 通常有一些做法可能富有成果, 而一些事情则没有.

有效构建机器学习算法的关键在于能找到一种方法来正确选择将时间投入何处.

通过诊断, 可以运行一个测试深入了解情况, 从而获得改进性能的指导. 诊断可能会需要一些时间来试试, 但运行诊断能在机器学习项目中很好地利用时间.

模型评估

将数据集分成一个训练集(training set)和一个单独的测试集(testing set), 可以系统地评估模型的学习成果如何. 通过计算测试误差和训练误差, 可以衡量算法在测试集和训练集上的表现.

一般将数据集分为70%的训练集和30%的测试集, 也可以分为80%的训练集和20%的测试集.

线性回归模型评估

计算测试集的成本函数误差, 特别注意没有正则化项.

计算训练集的成本函数误差, 特别注意没有正则化项.

可衡量算法在训练集和测试集上的表现, 且模型的泛化能力如何等等.

$J_{train}(\bold W, b)$训练集的误差越小, 表明参数w和b更拟合训练数据, 训练的误差可能远低于实际的泛化误差(不是训练集中新示例的平均误差).

$J_{test}(\bold W, b)$测试集的误差能测试算法在没有经过训练的示例上的性能, 这将更好地表明模型在新数据上的表现.

逻辑回归模型评估

计算测试集的逻辑损失函数误差, 特别注意没有正则化项.

计算训练集的逻辑损失函数误差, 特别注意没有正则化项.

通过查看测试错误方面的表现, 来确定学习算法是否运行良好.

分类问题除了计算逻辑损失误差的方法外, 还有下图(方框里)所示的方法

上图所示的方法不是使用逻辑损失来计算测试误差, 而是使用训练误差来衡量测试集的分数和算法错误分类的训练集的分数.

可以让算法对每个测试示例做出1或0的预测, 然后可在测试集中计算预测值y不等于测试集实际目标值的分数.

交叉验证

如果仅仅使用两个数据集(训练集和测试集), 并通过比较模型之间的$J_{test}(\bold W, b)$(通常误差最小的)来选择模型, 这个过程是有缺陷的, 可能会造成对泛化误差的乐观估计.

训练集$J_{train}(\bold W, b)$用来选择参数w和b, 训练集本身不能评估参数w和b的好坏, 因此使用测试集$J_{test}(\bold W, b)$来评估参数w和b的好坏.

同样的用测试集$J_{test}(\bold W, b)$来选择模型, 测试集本身不能评估模型的好坏, 因此上述评估模型的方法是有缺陷的.

因此引入了交叉验证(cross validation)集.

将数据分为三个不同的子集, 一个是训练集, 一个是交叉验证集, 一个是测试集. 通常划分比例是60%, 20%, 20%. 如下图所示

使用交叉验证集来检查不同模型的有效性或准确性.

交叉验证集, 可能被简称为验证集(validation set), 或开发集(dev set或development set). 计算公式如下图

同样的交叉验证集的误差计算没有正则化项.

交叉验证集的误差也简称为验证错误(validation error)或开发错误(dev error).

使用训练集训练好参数w和b后, 在交叉验证集上评估这些参数, 选择交叉验证误差最低的模型, 使用测试集计算泛化误差报告选择的模型在新数据上的表现.

同样也可以使用交叉验证集选择神经网络模型. 如下图

模型诊断

偏差和方差

偏差: bias 方差: variance, 如下图所示

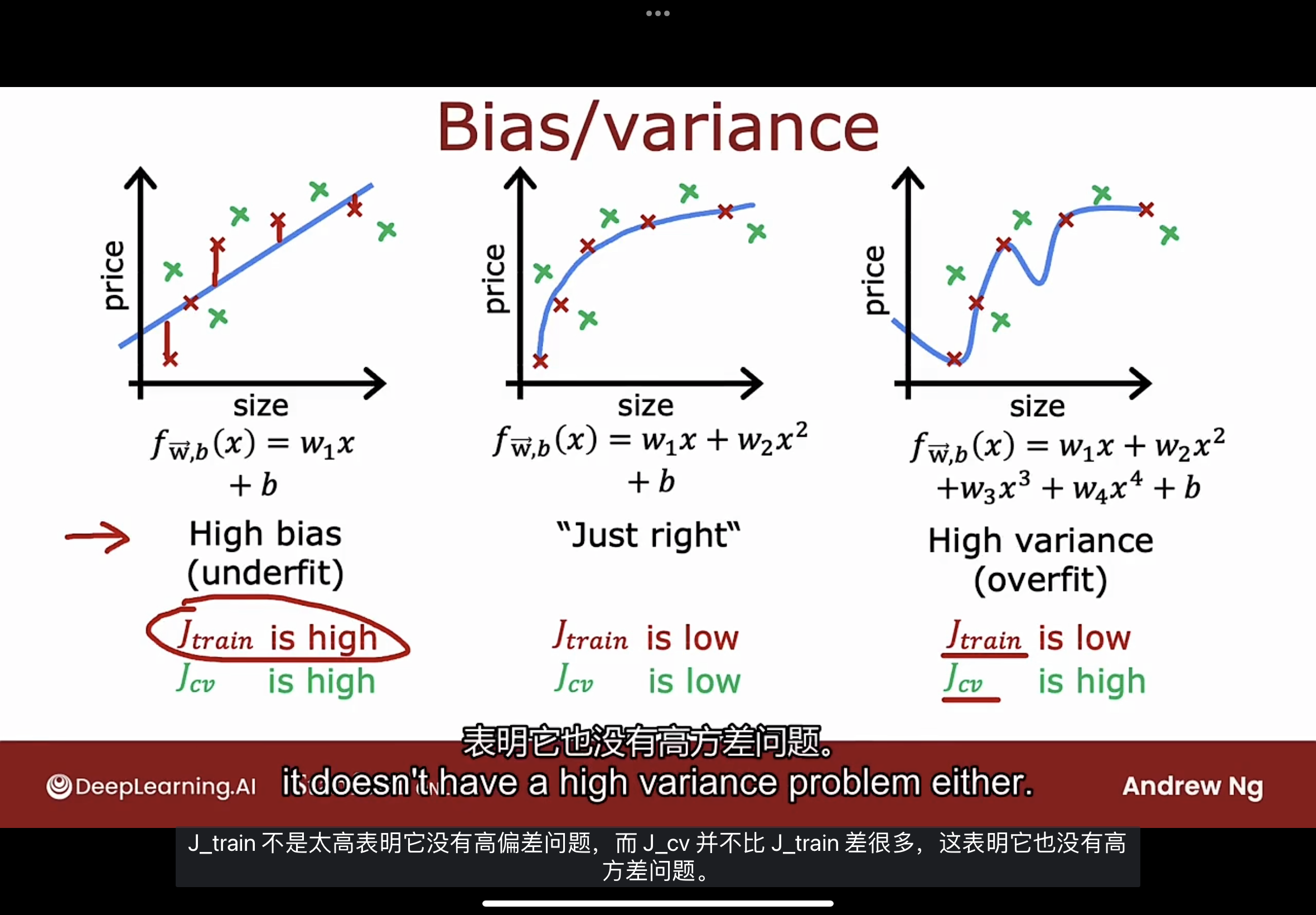
左边的模型是高偏差(High bias), 是欠拟合(underfit)的.

• 训练集$J_{train}$的误差高
• 交叉验证集$J_{cv}$的误差高, 但是和训练集$J_{train}$的误差是一个数量级的
• 这个模型在训练集上的表现不好, 且在新的示例数据上也表现不佳

而右边的模型是高方差(High variance), 是过拟合(overfit)的.

• 训练集$J_{train}$的误差小, 在训练集上的表现很好
• 交叉验证集$J_{cv}$的误差相当高, 在新的示例数据上做得不好

具有高偏差(欠拟合)的算法的一个特征是它在训练集上的表现太差. 因此当$J_{train}$很高时, 是该算法具有高偏差的有力指标.

算法具有高方差的特征是$J_{cv}$远高于$J_{train}$.

偏差和方差的图像如下图

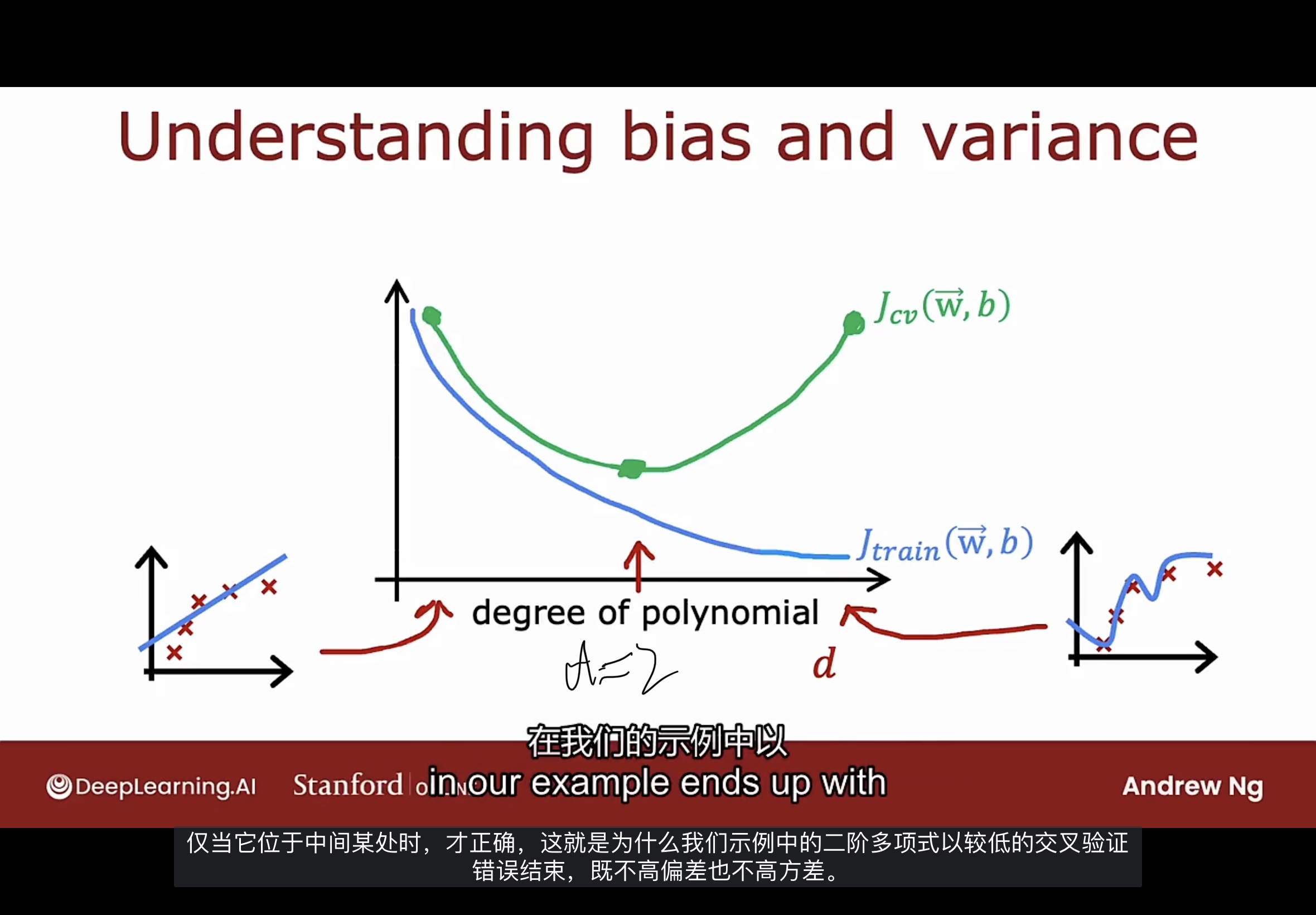
假设没有使用正则化, 注意横轴坐标上多项式的次数d, 曲线是$J_{cv}$和$J_{train}$随着次数d增加的变化.

随着多项式次数的增加, $J_{train}$通常会下降; 当次数低时, $J_{cv}$高(因为欠拟合), 当次数很大时, $J_{cv}$高, 在次数为2时, $J_{cv}$最低.

如何诊断学习算法是否有高偏差和高方差呢? 如下图

如果$J_{train}$高, 且$J_{cv}$和$J_{train}$相近, 是高偏差的表现.

如果$J_{train}$低, 且$J_{cv}$远大于$J_{train}$, 是高方差的表现.

如果$J_{train}$高, 且$J_{cv}$远大于$J_{train}$, 是算法既有高偏差也有高方差. 这种情况是算法过度拟合了部分训练数据, 由于某种原因, 对另一部分的训练数据是欠拟合的, 因此会造成高偏差和高方差.

正则化

正则化参数$\lambda$的选择是如何影响偏差和方差呢?

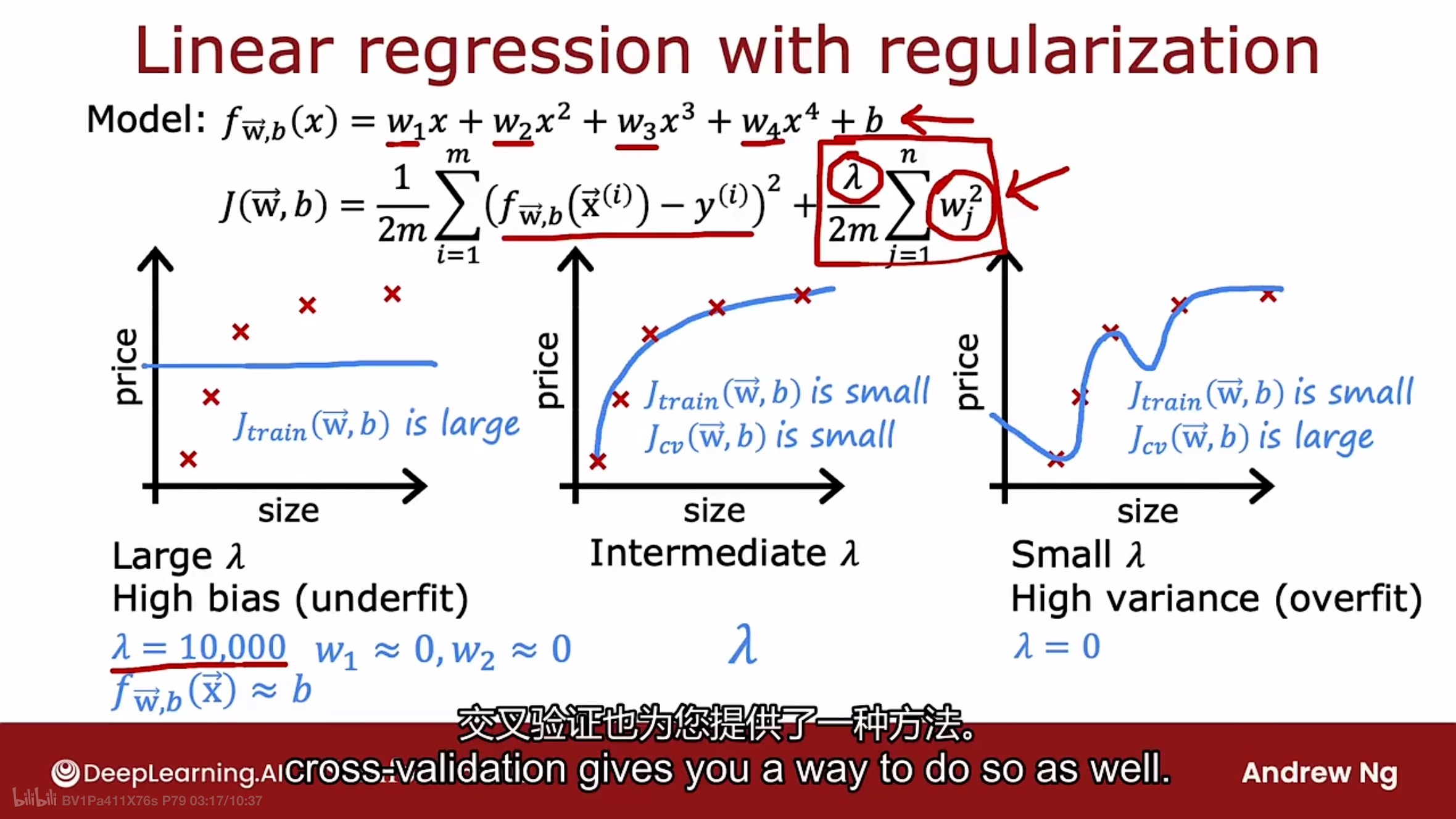
注意上图是在模型上多项式次数为4的时候的讨论.

如果正则化参数$\lambda$非常大, 那么算法就会保持这些参数w非常小接近于零, 于是导致模型函数像一条直线, 此时模型有高偏差(欠拟合).

如果正则化参数$\lambda$非常小, 那几乎等于没有正则化, 那会得到过度拟合数据的曲线, 于是导致模型具有高方差(过拟合).

因此交叉验证提供了一种用于选择良好的正则化参数$\lambda$的一种方法. 和选择参数w和b一样, 通过交叉验证的误差来进行选择.

如何理解这种选择? 如下图

注意大的坐标轴的横轴上正则化参数$\lambda$, 曲线是$J_{cv}$和$J_{train}$随着$\lambda$增加的变化.

可以看到, 当$\lambda$很小时, 模型具有高方差, 此时$J_{train}$很小, 而$J_{cv}$很大, $\lambda$在训练数据上表现很好, 但在交叉验证数据上表现很差.

当$\lambda$很大时, 模型具有高偏差, 此时$J_{train}$很大, 且$J_{cv}$也很大.

可以和右边小坐标轴对比着理解.

评估基准

基准性能水平(a baseline level of performance)是学习算法最终达到的合理的误差水平.

建立基准性能水平的方法:

1. 衡量人类在这项任务上的表现(比如语音识别, 人类的准确识别率才89.4%), 因为人类非常擅长处理非结构化数据(如语音, 图像, 文本)
2. 根据竞争对手的算法性能建立基准性能水平
3. 有时会根据以往的经验进行猜测

那怎么根据基准性能水平判断一个算法是否高偏差或高方差呢? 如下图

通过查看基准性能水平, 训练误差和交叉验证误差来判断.

如果训练误差和基准性能水平差距较小, 且训练误差和交叉验证误差较大, 那有高偏差问题.

如果训练误差和基准性能水平差距较大, 且训练误差和交叉验证误差较小, 那有高方差问题.

如果训练误差和基准性能水平差距较大, 且训练误差和交叉验证误差也较大, 那有高偏差和高方差问题.

学习曲线

说明

如下图的二阶多项式二次函数模型的学习曲线

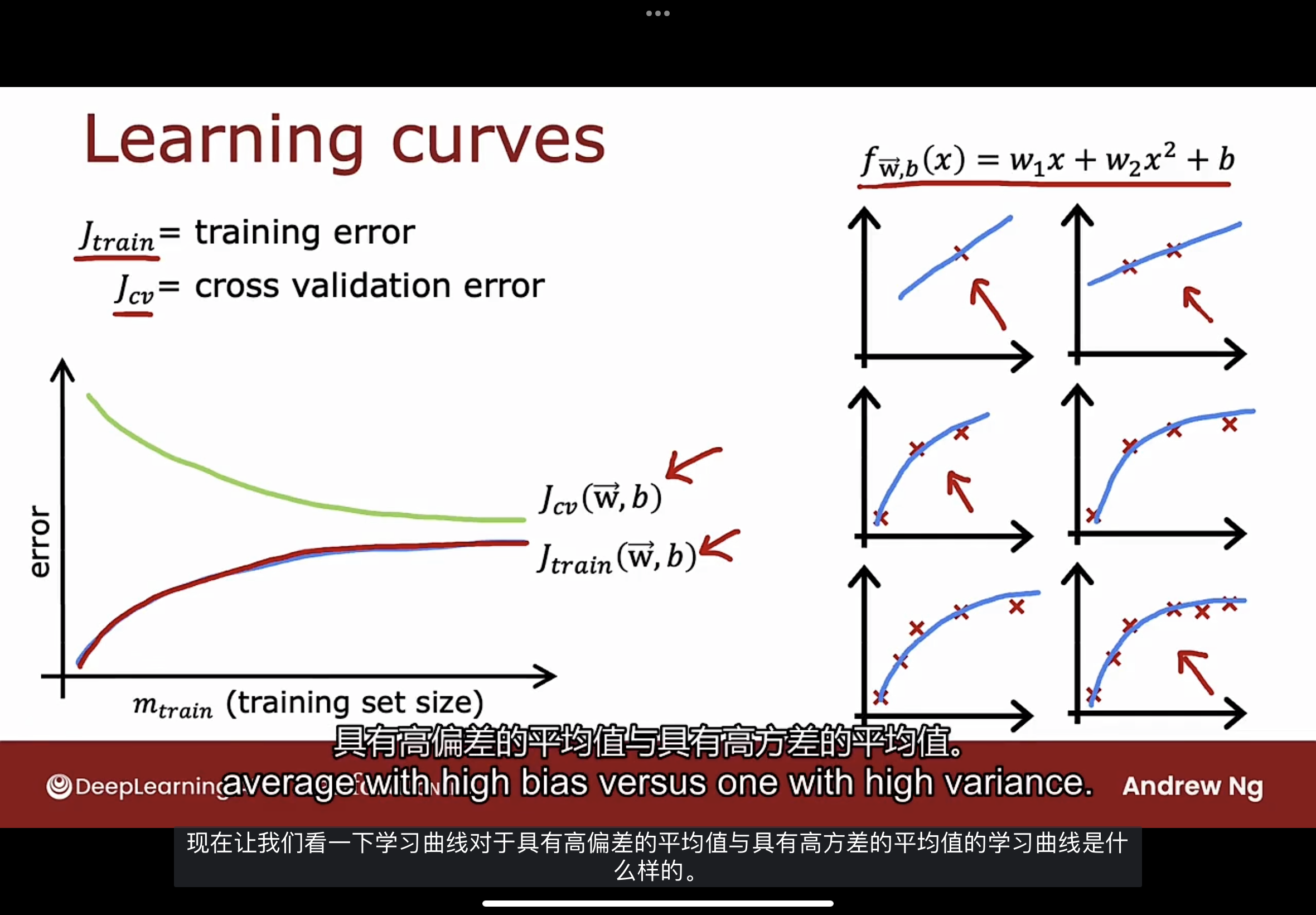
注意图中的坐标轴的横轴是训练集的大小m, 纵轴是误差.

随着训练集的增加, $J_{cv}$逐渐减小, 因为训练集越大, 能学习一个更好的模型, 因此交叉验证误差下降.

随着训练集的增加, $J_{train}$逐渐反而增大. 如图中右边所示, 因为当训练集很小时, 拟合为最简单的直线或曲线, 训练集误差几乎为零, 随着训练集的增加, 要完美地拟合所有训练数据更加困难, 此时训练集误差越来越上升.

图中的$J_{cv}$通常会高于$J_{train}$, 因为是拟合训练集的, 如果训练集很小, 模型在训练集上做的比在交叉验证集上做的更好.

高偏差示例

下图是个线性模型高偏差学习曲线的例子

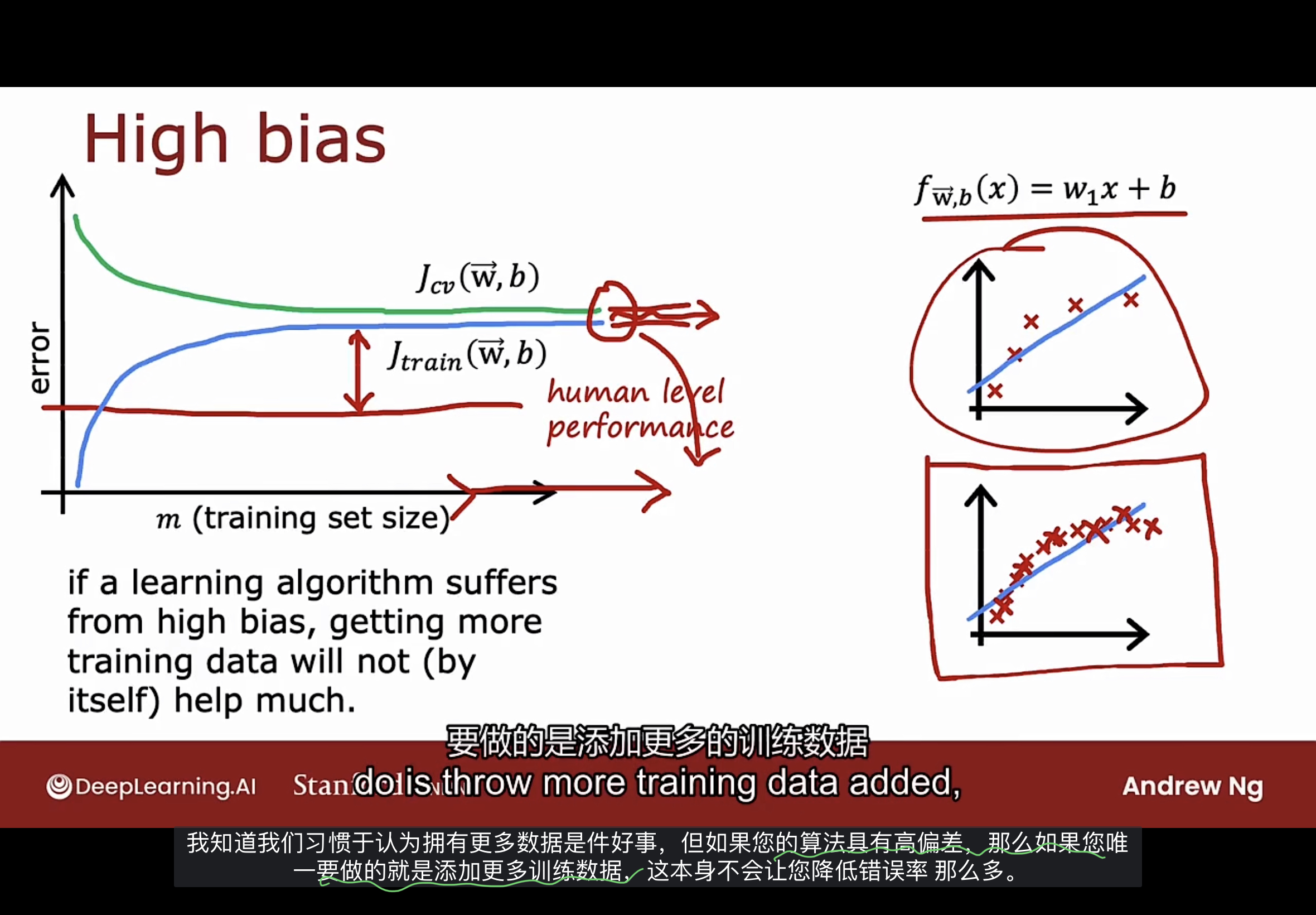
随着训练集的增加, $J_{train}$先上升, 然后逐渐平坦. 变得平坦的原因是在拟合简单的线性函数时得到更多的训练数据, 但模型实际上没有改变太多, 仅仅是直线斜率的一点变动.

同样的, 随着训练集的增加, $J_{cv}$先下降, 然后逐渐平坦, 但会高于$J_{train}$.

因为模型太简单了, 无法拟合更多的数据, 因此$J_{cv}$和$J_{train}$过一段时间后趋于平坦.

如果有衡量模型基线性能水平的方法, 比如人类的表现水平, 此时基线性能水平的值往往会低于$J_{cv}$和$J_{train}$.

基线性能水平与$J_{train}$之间存在很大差距, 是判断算法有高偏差的指标.

此时如果获取更多的训练集, $J_{cv}$和$J_{train}$的曲线向右变平延伸, 还会继续平坦. 这两条曲线无论如何都无法降低到基准性能水平(人类的表现水平).

可以得出结论: 如果算法具有高偏差, 获取更多的训练数据没有有效的帮助.

高方差示例

下图是个四阶多项式模型高方差学习曲线的例子

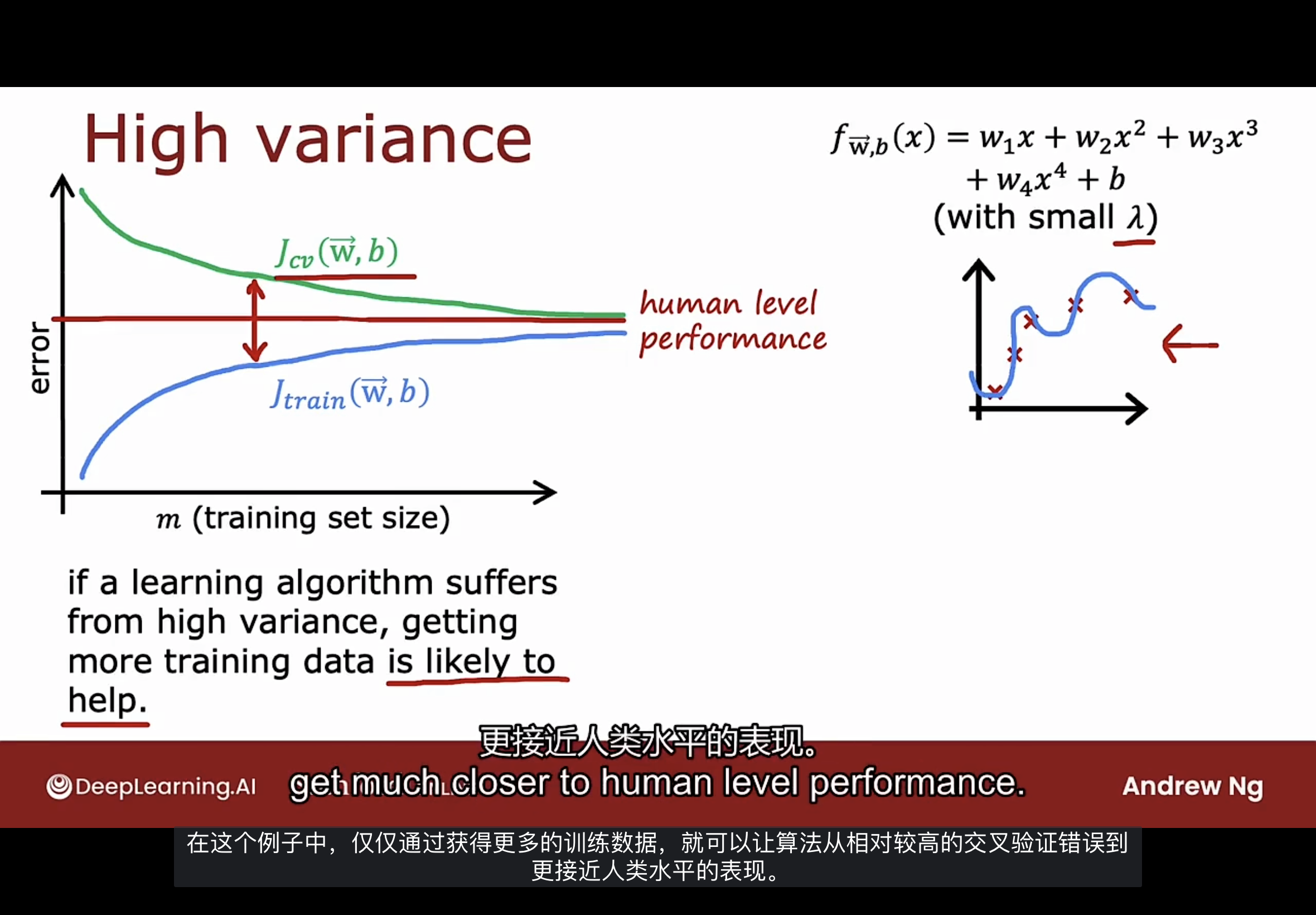
随着训练集的增加, $J_{train}$会随着增加而上升, 且$J_{cv}$要比$J_{train}$高得多.

如果有衡量模型基线性能水平的方法, 比如人类的表现水平, 此时基线性能水平的值往往介于$J_{cv}$和$J_{train}$之间.

$J_{cv}$与$J_{train}$之间存在很大差距, 是判断算法有高方差的指标.

当算法有高方差时, 增加训练集的大小会很有帮助. 随着训练集的增加, $J_{train}$将继续上升, 但是$J_{cv}$是下降的且越来越接近$J_{train}$.

添加更多的训练数据并继续填充该多项式, 可以更好的拟合训练数据, 曲线弯曲的程度会降低.

可以得出结论: 如果算法具有高方差, 获取更多的训练数据确实很有帮助.

做出决策

在训练学习算法时, 要经常地查看训练误差和交叉验证误差, 确定算法是否具有高偏差或高方差, 这将会帮助我们更好地决定下一步要做什么, 以提高算法的性能.

如下图, 使用的是预测房屋价格的例子来讨论如何做出决策

获取更多的数据

如果算法具有高偏差, 获取更多的训练数据, 可能不会有太大帮助.

如果算法具有高方差, 比如对非常小的训练集过度拟合, 那么获取更多的训练数据会很有帮助.

获取更多的训练数据有助于解决高方差问题

尝试缩小特征集

有时, 如果算法有太多的特征, 那么会给算法带来太多的灵活性, 来适应非常复杂的模型. 如果消除一些特征(如 $x^3$, $x^4$, $x^5$), 那么模型就不会那么复杂, 有助于降低灵活性和过拟合数据, 也不会有高方差.

消除或减少特征的数量有助于解决高方差问题

尝试增加额外的特征

如果不增加这些额外的特征(比如影响房价的卧室数量, 楼层, 房龄等), 算法永远都不会做得好. 添加了这些额外特征, 算法有了足够的信心, 可以在训练集上做得更好.

增加额外的特征有助于解决高偏差问题

尝试增加多项式特征

增加多项式特征, 能更好地拟合训练数据, 降低了$J_{train}$.

增加多项式特征有助于解决高偏差问题

尝试减少正则化参数$\lambda$

降低正则化参数$\lambda$意味着对正则化参数使用较低的值, 更关注在训练集上的拟合程度, 降低了$J_{train}$.

降低正则化参数$\lambda$有助于解决高偏差问题

尝试增加正则化参数$\lambda$

增加正则化参数$\lambda$意味着过度拟合数据. 过度拟合数据时, 增加正则化参数$\lambda$会减少对训练集的关注, 增加泛化到新示例的关注, 会迫使算法拟合更平滑的函数, 减少摆动, 解决高方差问题.

增加正则化参数$\lambda$有助于解决高方差问题

注意

无论如何, 通过减少训练数据来解决高偏差是没有帮助的.

如果减少训练集的大小, 算法会更好地拟合训练数据, 但往往会恶化交叉验证错误和学习算法的性能, 因此不要随意丢弃训练样本来试图修复高偏差问题.

忠告

偏差和方差时那些需要很短时间学习, 但需要一生才能掌握的概念和方法.

神经网络

偏差方差权衡(bias variance tradeoff): 如果模型太简单, 会有高偏差; 如果模型太复杂, 会有高方差, 必须在这之间找到权衡, 才能找到可能最好的结果.

实践证明, 在小型中等规模数据集上训练的大型神经网络是低偏差机器. 如果神经网络足够大, 总能很好地适应训练数据.

神经网络提供了一种新方法, 可以根据需要尝试减少偏差或减少方差, 无需真正在两者之间进行权衡. 如下图

步骤如下:

1. 神经网络首先在训练集上训练算法, 然后询问在训练集上的表示是否良好?
2. 测量$J_{train}$并查看相对于基准性能水平(人类表现水平)的高低, 如果表现不佳, 那么就会遇到高偏差问题(高训练误差). 此时减少偏差的一种方法是使用更大的神经网络, 即更多的隐藏层和隐藏神经元.
3. 可以继续步骤2的循环, 让你的神经网络越来越大, 直到它在训练集上表现良好.
4. 如果在训练集上的表现良好, 那么开始询问在交叉验证集上是否表现良好?
5. 测量$J_{cv}$看是否有高方差, 如果得出算法具有高方差. 此时减少方差的一种方法上获取更多的数据, 并重新训练模型并仔细检查.
6. 可以继续步骤5的循环, 直到最终它在交叉验证集上表现良好.
7. 然后你可能完成, 在一个交叉验证集上表现良好的模型, 并且希望能推广到新的示例数据中.

上述的步骤存在局限性, 训练更大的神经网络不会减少偏差, 但在某些时候确实会增加计算成本, 这也是神经网络的兴起确实得益于运算速度很快的计算机, 尤其是GPU. 即使硬件加速器超过一定程度, 神经网络也非常庞大, 训练需要很长时间, 逐渐变得不可行.

另一个局限性是获取更多的数据, 有时你只能得到这么多的数据, 超过某个点就很难得到更多的数据. 更多的数据解释了深度学习为何适用于可以访问大量数据的应用程序.

如果神经网络太大怎么办, 会产生高方差问题吗?

实践证明, 具有精心选择的正则化的大型神经网络通常与较小的神经网络一样好甚至更好. 大型神经网络会减慢训练和推理过程, 计算成本较高.

在代码中使用正则化

# 没有使用正则化的神经网络
layer_1 = Dense (units=25, activation="relu")
layer_2 = Dense (units=15, activation="relu")
layer 3 = Dense (units=1, activation="sigmoid")
model = Sequential([layer_1, layer_2, layer_3])

# 使用了正则化的神经网络
# 方法参数kernel_regularizer中的数字0.01是正则化参数
# 可以为不同的神经网络层选择不同的正则化参数
layer_1 = Dense(units=25, activation="relu", kernel_regularizer=L2 (0.01))
layer_2 = Dense(units=15, activation="relu", kernel_regularizer=L2(0.02))
layer_3 = Dense(units=1, activation="sigmoid", kernel_regularizer=L2(0.03))
model = Sequential([laver_1, laver_2, laxer_3])

开发机器学习系统

以下图的垃圾邮件分类开发为例进行说明

该垃圾邮件分类列举1万个单词作为输入特征, 并统计这些单词在垃圾邮件中出现的次数作为训练数据. 输出结果是1(垃圾邮件)或0(非垃圾邮件).

上图是进行一次诊断后, 根据诊断的结果可做出的下一步解决方案的列表.

机器学习开发的迭代

首先, 决定系统的总体架构是什么, 包括模型, 数据, 参数等等.

然后根据架构, 实施和训练模型, 但第一次训练模型, 模型几乎不会按你想要的那样工作.

下一步是实施或查看一些诊断, 比如算法的偏差和方差, 以及错误分析. 根据诊断, 可以做出下一步的决定, 如是否扩大神经网络, 是否更改正则化参数, 是否添加更多的数据, 是否增加或减少特征集等等.

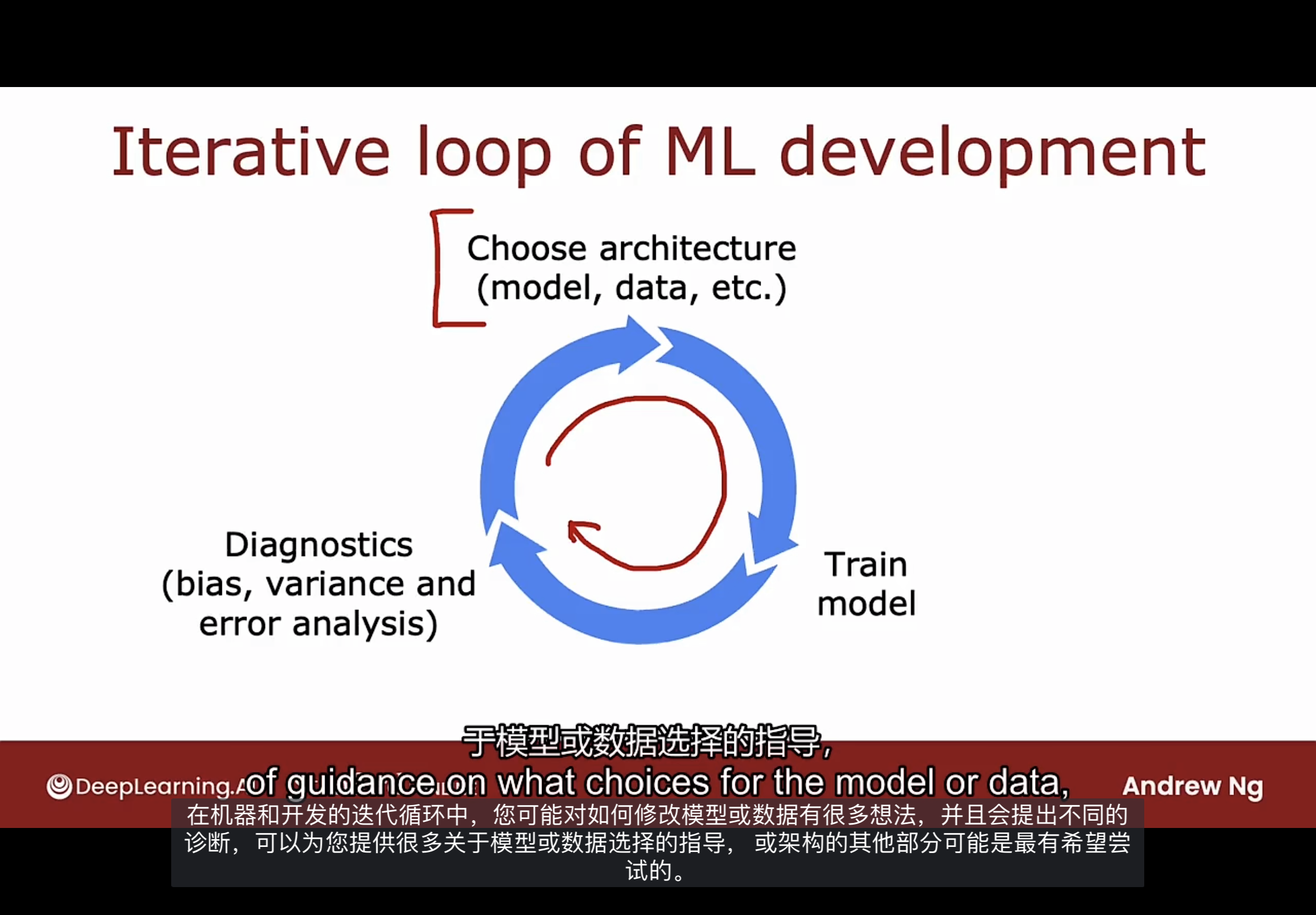
然后选择新的体系结构再次开始迭代, 并且进行多次迭代, 直到达到您想要的性能.

错误分析

运行诊断, 帮助提高学习算法性能的方法除了偏差和方差(最重要)分析外, 错误分析可排在其次. 下图是对垃圾邮件分类的错误分析

假设有500个的交叉验证示例, 且算法错误分类了这500个中的100个.

错误分析是指手动查看这100个示例, 并深入了解算法出错的地方. 把算法错误分类的示例, 尝试将它们分组为相同的主题或共同的特征或共同的属性.

最终得到错误分类在这些不同主题的统计数字, 如上图所示. 药物垃圾邮件和试图窃取密码钓鱼邮件是较大的问题, 而故意拼写错误是一个较小的问题.

错误分析告诉您, 即使您构建非常复杂的算法来查找故意拼写错误, 它也只能解决100个错误分类示例中的3个.

错误分析可确定问题的优先级高低, 从而使算法性能更高.

注意: 错误分类示例在分组的主题或特征或属性上上可以重叠的, 不是互相排斥的. 例如可能有一封药物垃圾邮件也有不寻常的路由, 故意拼写错误, 网络钓鱼攻击的属性.

如果交叉验证集很大, 算法错误分类示例也很大, 那可能没有时间全部手动查看所有的算法错误分类示例. 这种情况下, 可以随机抽取大约100个示例(能在合理的时间内查看的数量)进行错误分析. 这随机抽取的100个示例能提供足够的统计数据, 了解是否是最常见的错误类型, 以及集中注意力解决最有成效的问题.

经过错误分析, 发现很多错误说医药垃圾邮件.

1. 可能决定收集数据, 但不是收集所有的数据, 而是针对性的收集医药垃圾邮件数据, 以便算法可以更好地识别这种类型的垃圾邮件.
2. 可能决定添加一些与药物特定名称相关的新特征, 以帮助算法可以更好地识别此类垃圾邮件.

因此, 错误分析的要点是通过手动检查算法错误分类的一组示例, 能为下一步的尝试创造灵感, 有时还可以得知某些类型的错误非常罕见, 不值得花费太多的时间来修复.

错误分析的一个局限性是更容易解决人类擅长的问题, 对于人类不擅长的任务, 错误分析可能会更难一些.

有效添加数据

训练机器学习算法是, 总希望能一直有更多的数据, 有时很想获取所有内容的更多数据, 但是尝试获取更多所有类型的数据可能既慢又贵.

针对性添加

添加数据的一种方法是专注于添加通过错误分析得到更有帮助的类型的数据. 比如上一节的错误分析认为医药垃圾邮件是问题, 要针对性的解决, 因此专注于获取更多医药垃圾邮件示例. 只需要添加这种类型的邮件示例, 能使算法更聪明地识别医药垃圾邮件.

如果有大量的未标记的电子邮件数据, 需要工作人员通过未标记的数据找到更多医药垃圾邮件的示例, 这可以大大提高学习算法性能, 而不是添加更多各种电子邮件数据.

数据增加

数据增加(Data augmentation)是一种从现有的训练示例来创建一个新的训练示例的技术.

比如上图识别字母的学习算法, 通过稍微旋转图像, 或将图片放大缩小一点, 或改变图像的对比度, 这是图像扭曲的例子, 这样做不会改变图片中的字母A看起来还是未修改前字母A的事实, 而不是其他字母.

对输入X应用失真或变换, 以得出另一个具有相同标签的示例, 通过这样做, 可告诉算法字母A旋转了一点, 放大缩小了一点, 但还是字母A. 通过这样的方式可以让算法更好地学习识别字母A.

数据增加的更高级示例, 是在字母A上放置一个网格, 如下图

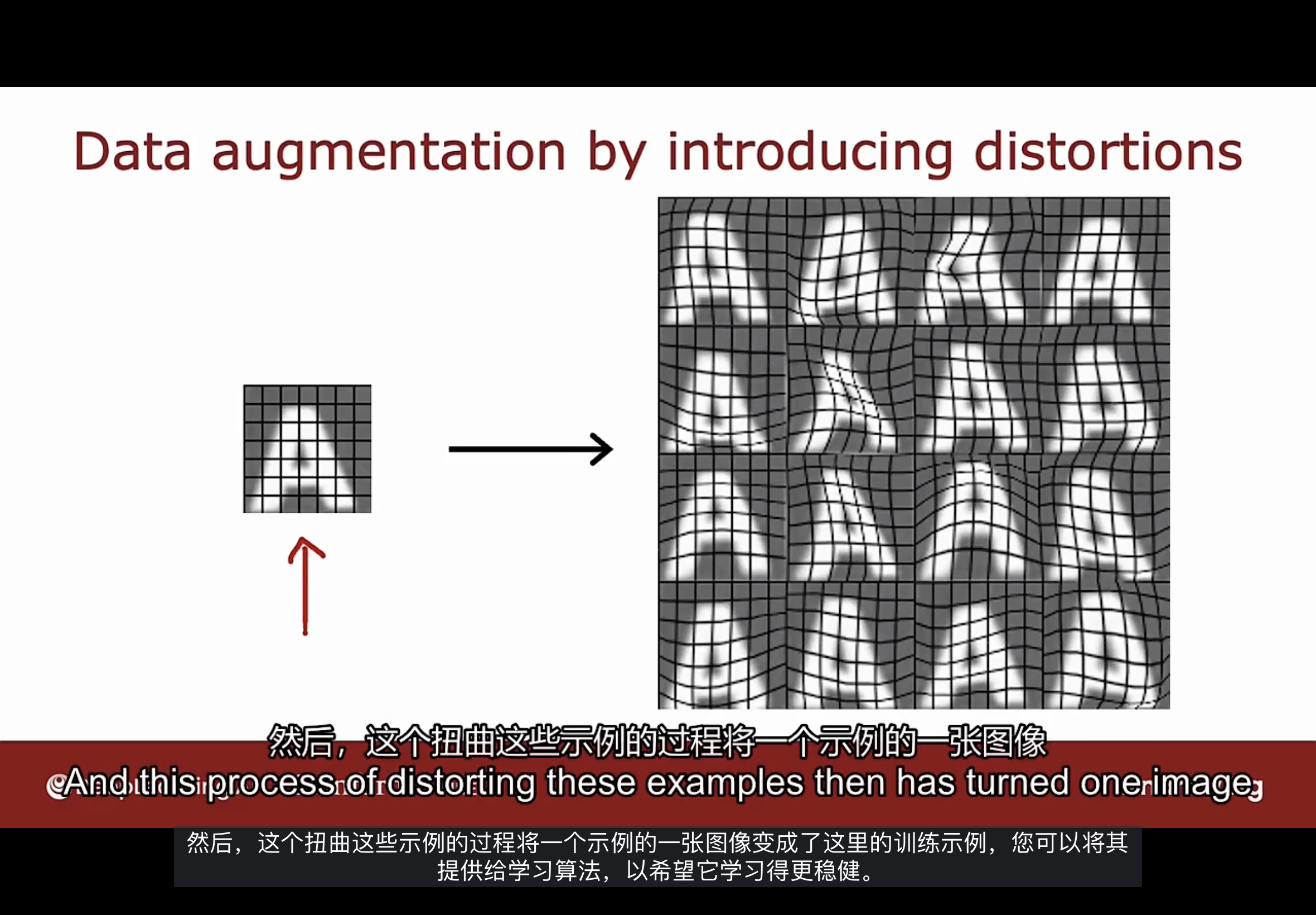
通过扭曲, 将一个示例的图像变成了这里的训练示例, 可将其提供给学习算法, 希望学习算法能够更加稳健.

这种数据增加的想法也适用于语音识别. 如下图

将原始语音应用于语音数据的一种方法是获取嘈杂的背景音频.

通过音频剪辑, 把原始语音和人群嘈杂的音频组合, 感觉像是在人群嘈杂的背景中说话的.

通过不同的背景噪音(比如车里, 信号连接不好)和原始语音的合成, 模拟人说话的环境声, 从而得到更多的语音训练数据, 这是一种非常关键的技术, 可以人为增加必须构建更准确语音识别的训练数据的大小.

数据增加的一个技巧是对数据所做的更改或扭曲应该代表测试集中噪音或扭曲的类型, 即希望在测试集中让算法学习到什么类型. 相比之下, 对于数据纯粹随机无意义的噪音通常没有多大帮助.

Distortion introduced should be representation of the type of noise/distortions in the test set.

数据合成

数据合成(Data synthesis): 使用人为的数据输入创建全新的训练示例. 不是通过修改现有的示例, 而是通过创建全新的示例. 如下图的图像识别

为这项任务创建人工数据的一种方法是, 使用计算机携带的字体, 随机文本, 使用不同的颜色, 不同的对比度生成图片, 截取这些图片, 会得到像右边的合成数据.

编写代码为给定的应用程序生成这些看起来逼真的合成数据可能需要做很多工作, 但是花时间这样做, 有时可以帮助为应用程序生成大量数据, 并极大地提升算法性能.

合成数据最有可能用于计算机视觉(Computer Vision), 而较少用于其他应用程序.

在机器学习兴起的早期, 大多数机器学习研究人员的注意力集中在传统的以模型为中心的方法上.

如今的算法已经足够强大, 且适用于多数类型的应用程序, 因此有时花更多时间采用以数据为中心的方法会更有成效.

迁移学习

Transfer Learning

对于没有那么多数据的应用程序, 迁移学习上一种很棒的技术, 能使用来自不同任务的数据来帮助你的应用程序.

定义

如下图示例解释迁移学习

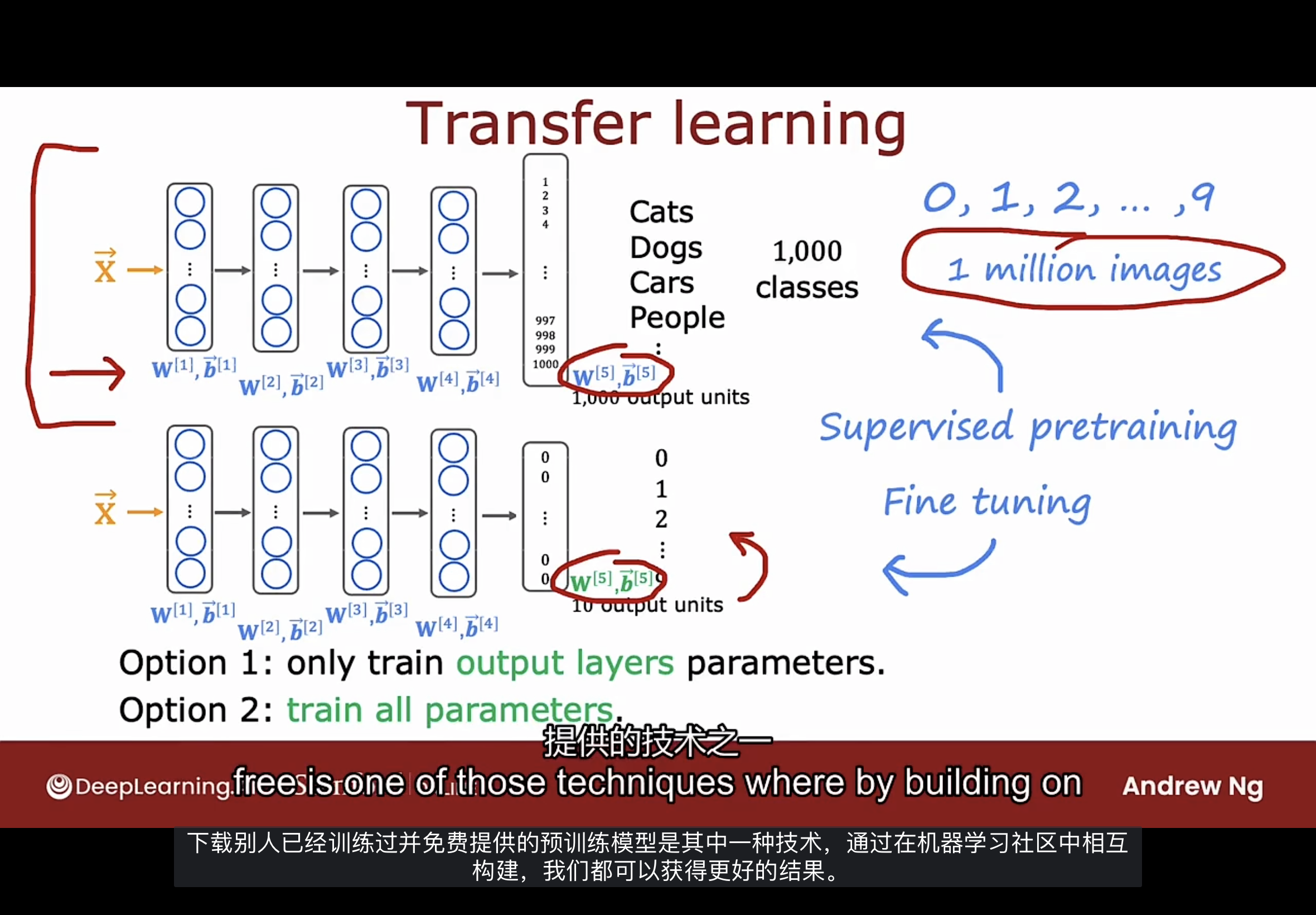
假设要训练一个识别从0到9的手写数字识别模型, 但没有这么多的标记数据.

假如有一个一千个不同类别且在大型数据集上训练好的神经网络.

要应用迁移学习, 要做的是复制此神经网络, 以及隐藏层的参数w和b, 但要消除原神经网络的输出层, 用一个更小的输出层(只有10个输出单元, 对应要识别的手写数字0-9)替换, 输出层的参数无法复制过来, 因为该层的维度已更改, 因此需要需要从头开始训练新的参数w和b.

这种算法称为迁移学习, 直觉是通过学习识别其他类别, 希望它已经为处理图像输入的早期层学习了一些合理的参数集, 然后通过这些参数转移到新的神经网络, 新的神经网络从一个更好的地方开始训练, 只需一点的学习, 能最终使新的神经网络成为一个非常好的模型.

如何训练新的神经网络?

方法1: 只训练输出层的参数, 该方法适用于训练集非常小的

方法2: 训练所有层的参数, 该方法适用于训练集稍微大一点的

监督预训练(Supervised Pretraining): 先在大型数据集上进行训练的步骤

调优(Fine Tuning): 可从从监督预训练中获取参数, 进一步运行梯度下降或Adam优化算法微调参数以适应新的应用程序.

迁移学习的好处是不需要进行监督预训练的步骤, 对于许多神经网络, 有研究人员已经在大图像集中训练了一个神经网络, 并在Internet上发布, 免费授权给任何人下载和使用.

只需下载网上的神经网络, 然后将输出层替换为自己的输出层, 并执行方法1或方法2即可调整别人已经经过监督预训练的神经网络, 只需要做一点微调就可以快速得到一个在你的任务上表现良好的神经网络.

原理

为何迁移学习如此有效? 如下图

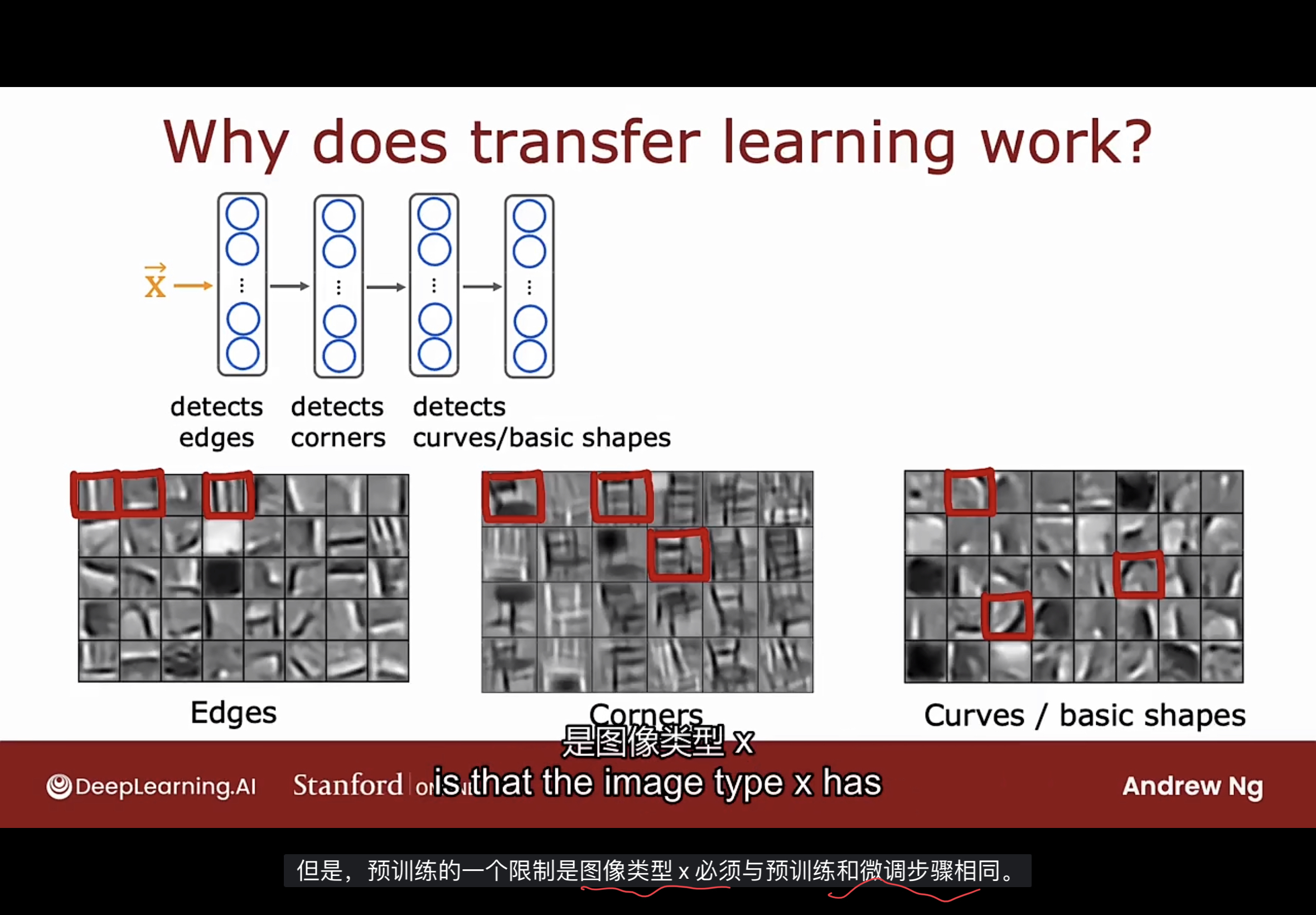
通过学习检测大量不同的图像, 实际上是帮助神经网络检测非常通用的图像特征, 如边缘, 角落和基本形状. 这对于许多其他计算机视觉任务很有用.

但预训练的一个限制是图像类型(输入数据X)必须与预训练和微调步骤相同. 如果目标是构建一个语音识别系统来处理音频, 那么在图像上预训练的神经网络可能不会对音频有太大帮助, 相反, 您需要一个在音频数据上进行预训练的神经网络.

总结

实施迁移学习的步骤, 如下图

步骤1: 下载带参数的神经网络, 其参数已在与您的应用程序具有相同输入类型的大型数据集上进行了预训练.

步骤2: 然后根据您自己的数据进一步训练或微调网络.

迁移学习可以在机器学习社区彼此共享想法, 代码和训练参数. 在机器学习中, 我们所有人最终往往建立在彼此工作的基础上, 开放和共享想法, 代码和训练参数是机器学习社区的一种方式, 我们所有人共同努力做的更好.

吴恩达希望加入机器学习社区的你有一天也能找到一种方法来回馈社区.

项目周期和部署

项目周期

机器学习项目的周期如下图所示

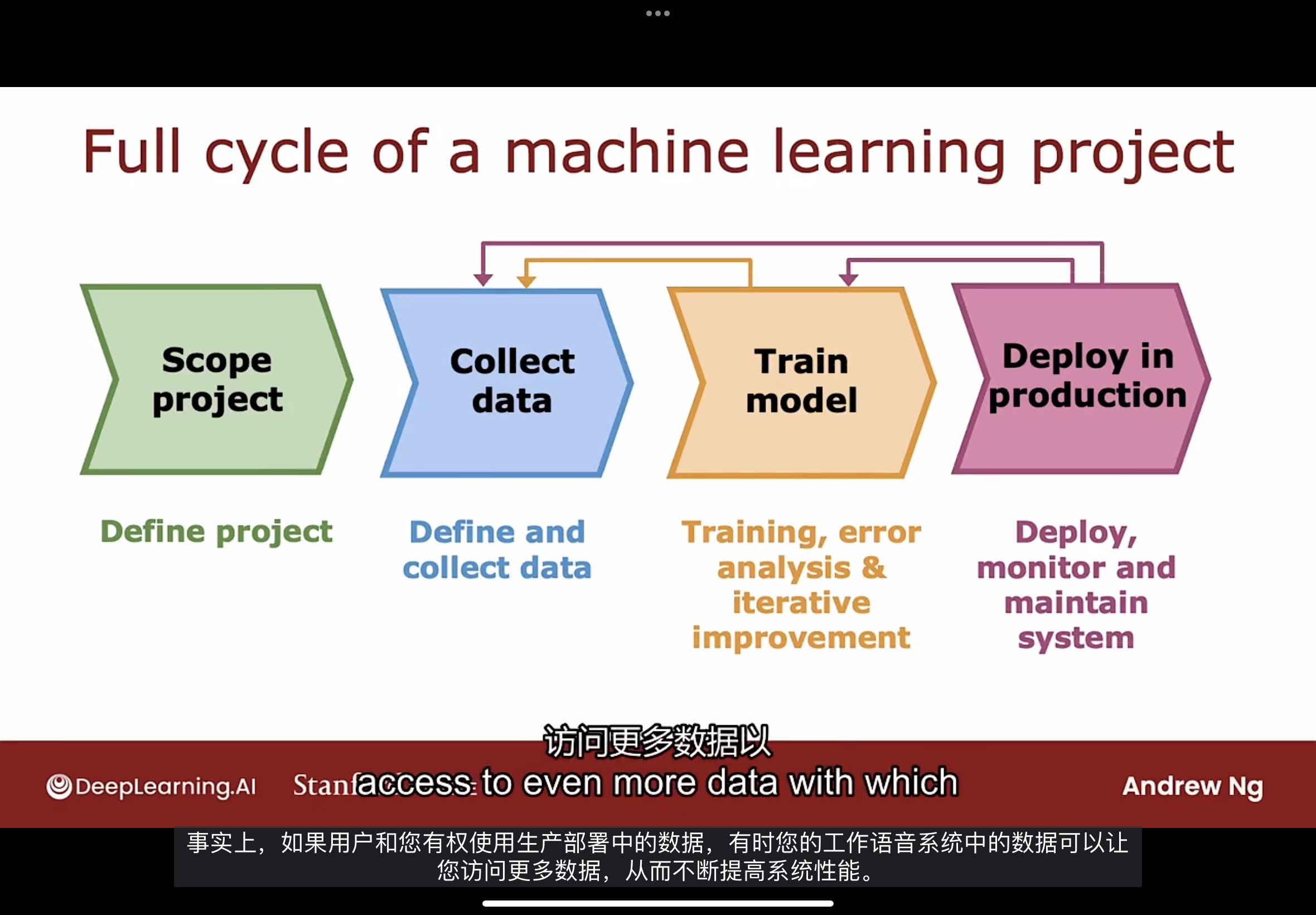
第一步: 确定项目范围, 决定项目做什么和怎么做此项目.

第二步: 确定训练机器学习系统所需的数据并收集数据.

第三步: 然后可以开始训练模型, 并通过偏差和方差, 错误分析等工具改进迭代模型.

在开始训练模型进行错误分析或偏差-方差分析后, 可能会想返回以收集更多数据. 也许是收集更多的所有数据或者只是收集更多特定类型的数据, 这将由错误分析诊断出.

第四步: 经过上述步骤一段时间, 直到模型足够好, 然后在生产环境中部署. 当部署一个系统时, 还必须确保继续监控系统的性能并维护系统以防性能变差, 而不仅仅在服务器上托管你的机器学习模型.

这次部署之后, 有时可能会意识到模型并没有按要求工作, 会回去训练模型再次改进它, 甚至是回去获取更过数据.

项目部署

下图显示了机器学习项目部署的情况

训练了一个高性能的机器学习模型之后, 部署该模型的一种常见方法是采用此机器学习模型并在推理服务器中实施它.

推理服务器(Inference Server)是负责调用机器学习模型的, 并返回模型预测结果.

如果团队中已经实现了一个移动应用程序, 那么该应用程序可以进行API调用, 把录制的音频剪辑发给推理服务器, 然后推理服务器调用学习模型进行预测并将结果(文本抄本, text transcript)返回给应用程序.

这是常见的模式, 有一个API调用, 可以为学习模型提供输入X, 学习模型做出预测并输出y_hat.

为了实现上述的方式, 可能需要一些软件工程师来编写完成这些事情的所有代码.

根据应用程序提供服务的用户数量多少, 可能所需的软件工程师数量会大不相同.

根据所需的规模应用:

1. 可能需要软件工程来确保推理服务器能够对不太高的计算成本做出可靠和有效的预测

2. 可能需要软件工程来管理对大量用户的扩展

3. 可能需要软件工程记录输入X和输出y_hat的数据, 假设用户隐私同意存储此数据

4. 可能需要进行系统监控, 监控系统能清楚知道数据何时发生变化和算法何时变得不那么准确, 这能及时重新训练模型, 然后执行模型更新替换旧模型

机器学习中有一个不断发展的领域, 叫做MLOps(Machine Learning Operations). 这是指如何系统地构建, 部署和维护机器学习系统的实践. 做上述的所有事情以确保机器学习模型可靠, 可扩展, 具有良好的伸缩性, 受到监控, 然后有机会根据需要对模型进行更新以保持其良好运行.

机器学习伦理

吴恩达希望, 如果您正在构建一个影响人们的机器学习系统, 要确保您的系统相当公平, 合理, 且没有偏见, 并采取合乎道德的方法.

请不要构建对社会有负面影响的机器学习系统. 如果您被要求进行开发一个您认为不道德的机器学习系统, 敦促您为了它的价值而走开.

一些让您的系统更公平, 更少偏见和更合乎道德的建议:

1. 组建一个多元化的团队来集思广益可能会出错的事情, 并强调可能造成的伤害.
2. 对您所在的行业和特定应用领域的标准和指南进行文献搜索, 这样构建的系统更合理公平且没有偏见.
3. 在部署之前, 对系统进行衡量, 看它是否真的存在对某些性别或种族或其他群体的偏见, 确保发现并解决.
4. 可以使用缓解计划回滚到早期认为是相当公平的系统, 在部署之后, 继续监控系统是否出现危害, 以便可以触发缓解计划并迅速采取行动.

发现这些问题, 并在它们造成伤害之前解决它们, 这样我们就可以共同避免机器学习界以前犯过的一些错误, 因为这些东西很重要, 我们构建的系统可以影响很多人.

倾斜数据集

如果您正在开发一个机器学习应用, 其中正例和负例的比例非常倾斜, 那么通常的错误指标(如准确率)效果不佳.

下面的说明都是以诊断极其罕见疾病的二元分类问题为例子

误差指标

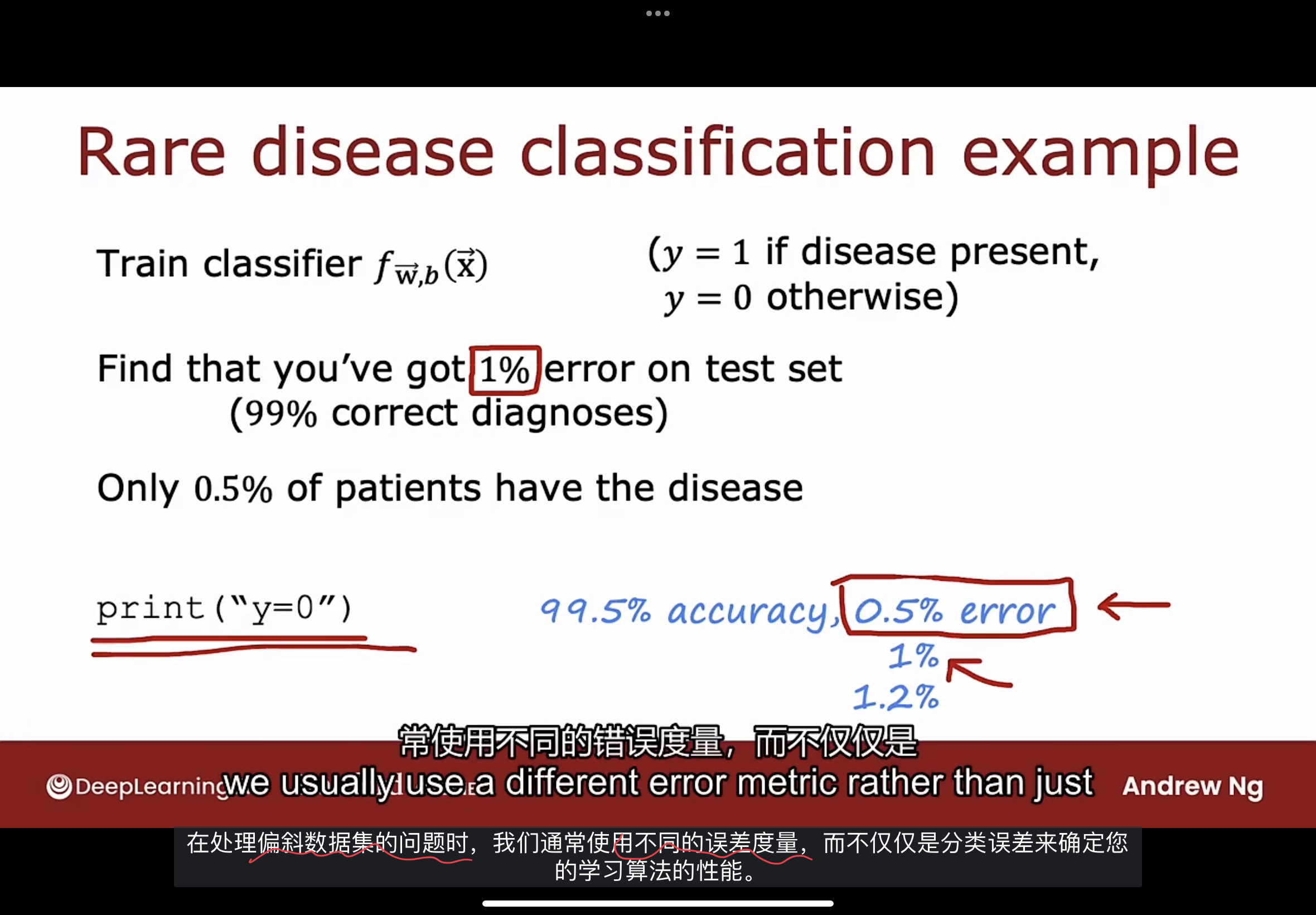
如上图所示, 如果预测y为1, 则有该疾病, 0则是其他情况.

假如训练了一个模型, 在测试集上有99%的准确率, 有1%的错误率.

但实际人群中患这种疾病的概率是99.5%.

还有一个一直打印y=0的程序, 始终预测y等于0, 这程序实际上有99.5%的准确率和0.5%的错误率.

于是得出一个一直打印y=0的程序算法优于您的学习算法, 因为它错误率有0.5%比1%要小.

我们都知道, 一直打印y=0的程序不是一个好的算法, 这也意味着您无法判断得到1%的错误率是好结果还是坏结果. 因为误差最小的预测可能不是有效的预测, 像这样总是预测y等于0并且永远不会诊断任何患者患有这种疾病.

在处理偏斜数据集的问题时, 通常使用不同的误差度量, 而不仅仅是分类误差来确定学习算法的性能,

针对这种问题的常见错误指标是准确率(Precision)和召回率(Recall).

精度和召回率

如上图所示, 根据实际分类结果和预测分类结果构建一个混淆矩阵.

假如有100个交叉验证示例:

1. 其中15个学习算法预测1的数量和实际分类标签1的一致, 称为True Positive.
2. 其中5个学习算法预测为1的数量, 而实际分类标签为0的, 称为False Positive.
3. 其中25个学习算法预测为0的数量, 而实际分类标签为1的, 称为False Negative.
4. 其中70个学习算法预测为0的数量和实际分类标签1的一致, 称为True Negative.

将分类划分为这四个单元后, 可能会计算的两个常见指标是精度和召回率.

学习算法的精度计算的是算法预测的所有患病患者中有多少是实际上是真的患病的. 如上图所示, 得出这个算法的精度有75%. 意味着在它认为患有这种罕见疾病的所有患者(预测患病的)中, 有75%是实际上真的患病的.

学习算法的召回率计算是实际上真的患病患者中有多少是被学习算法预测到了. 如上图所示, 得出这个算法的召回率有60%. 意味着在实际上真的患有这种罕见疾病的患者中, 算法能预测到60%.

精度和召回率能帮助检测学习算法是否一直打印y=0, 如果一直预测为0, 那么精度和召回率都将为0.

在实践中, 如果一个算法连一个正例都没有预测到, 也可以说精度为0.

一般来说, 零精度或灵召回率的学习算法不是有用的算法.

权衡精度和召回率

高精度意味着如果患者被诊断患有这种罕见疾病, 那么该患者可能确实患有这种疾病.

高召回率意味着如果有患者患有这种罕见疾病, 算法可能会正确识别出他们确实患有这种疾病.

在实践中, 精度和召回率之间往往需要权衡取舍.

提高阈值

假设每当我们预测患者患有罕见疾病时, 我们可能不得不将他们送去接受有创且昂贵的治疗.

如果疾病的后果不是那么糟糕, 即使没有积极治疗也不会影响患者生活, 那么只有我们非常有信心的情况下, 才可能希望预测y等于1.

这种情况下, 可以设置一个更高的阈值, 只有当f大于等于该阈值时才会预测为1. 注意预测1和0的阈值必须相同, 因为是根据此阈值来预测是0还是1.

提高阈值会导致较高的精度, 但是会导致较低的召回率.

降低阈值

假设我们想避免遗漏太多罕见病病例, 或者患者疑似有罕见病时预测为1, 这种疾病如果不治疗这会给患者带来更糟糕的后果. 这种情况下, 出于安全考虑, 预测这些患者患有该疾病, 并考虑治疗.

这种情况下, 可以设置一个更低的阈值, 只要算法认为该疾病存在的可能性为该阈值或更高, 就可以预测为1, 并且只有非常确定该疾病不存在时, 才预测为0.

降低阈值会导致较低的精度, 但是会导致较高的召回率.

更一般的说

只有当f高于某个阈值的时候, 才预测一个, 并且通过选择该阈值, 可以在精度和召回率之间做出不同的权衡.

精度和召回率的曲线如上图的坐标轴所示.

对于许多应用程序, 手动选择阈值以权衡精度和召回率是最终要做的.

如果你想自动权衡精度和召回率, 而不是自己手动选择, 有称为F1 score的指标自动结合精度, 召回率帮助选择最有价值的或最佳平衡.

F1 Score指标

如上图所示, 将精度和召回率加在一起取平均值的方法不是一个好方法. 比如对于图上的算法3, 其平均值最高, 但实际上精度很低, 召回率完美, 意味着该算法几乎诊断所有的患者都有此罕见疾病.

F1 Score指标是一种计算平均分数的方法, 它更关注较低的分数. 公式如下

$F1 score = \frac{1}{\frac{1}{2}(\frac{1}{P}+\frac{1}{R})}=2\frac{PR}{P+R}$

其中P说精度, R是召回率.

这种公式也被称为P和R的调和平均数, 调和平均数是一种取平均值的方法, 更强调较小的值.

决策树模型

Decision Tree

以判断是不是猫的二元分类问题作为示例, 数据如下图

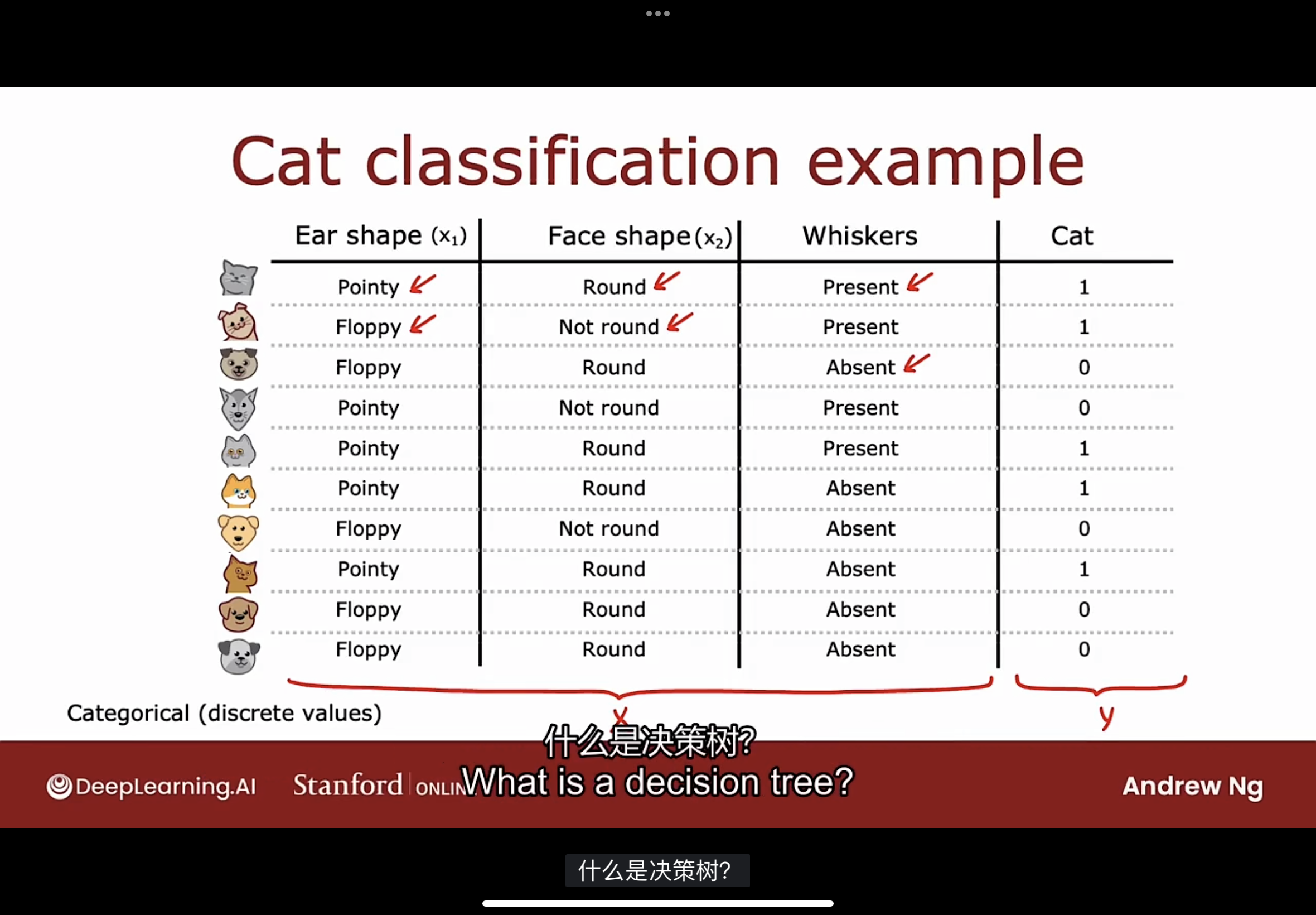
在此示例中, 输入特征X具有分类值, 也就是每个特征的具有几个离散值(猫的耳朵要么是尖的-Pointy, 要么是松软的-Floppy).

这是一个二元分类任务, 因为标签的值是1或0.

定义

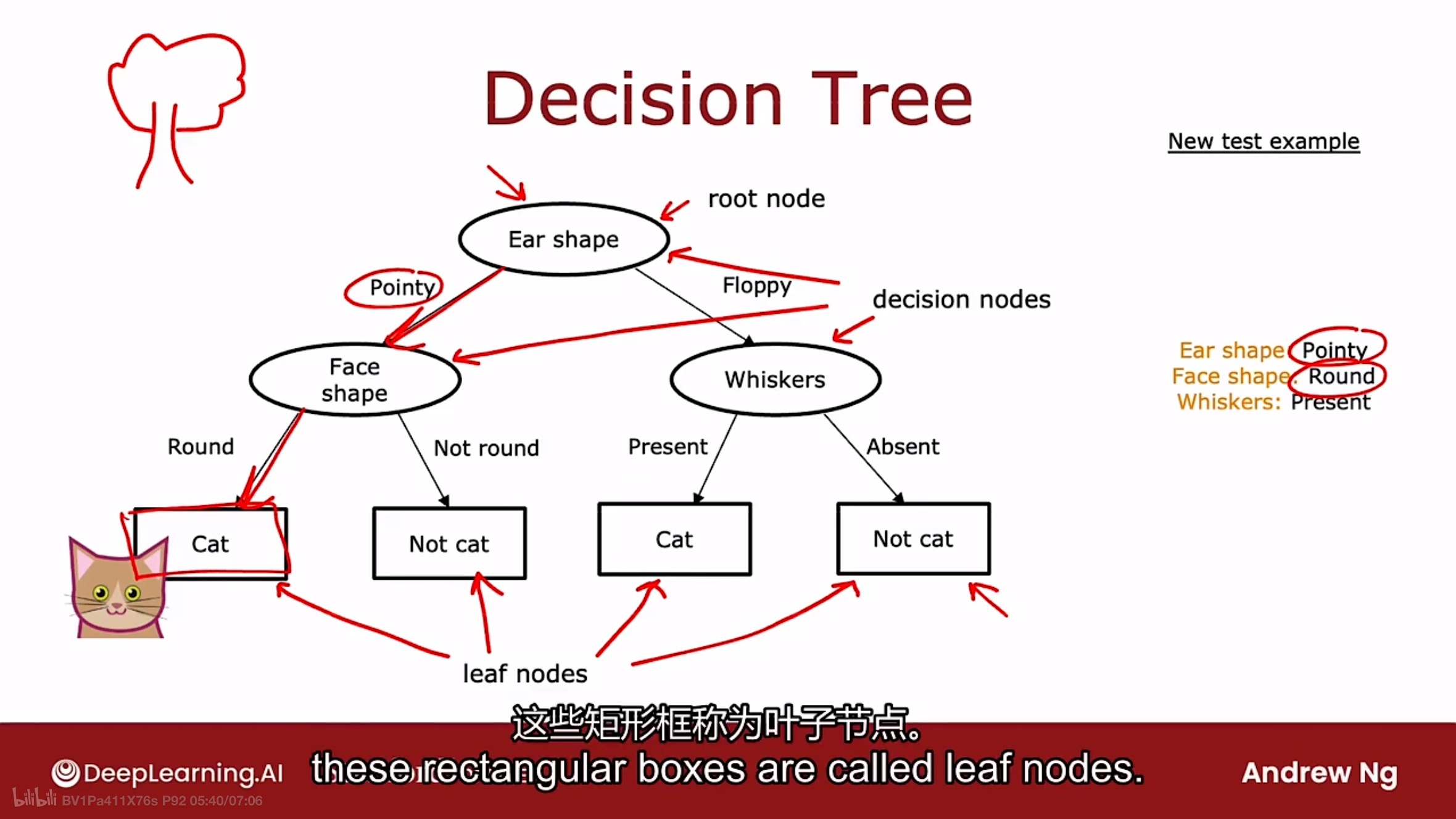
如上图所示, 在数据集上训练决策树学习算法后可能获得的模型.

学习算法输出的模型看起来像一颗倒立的数据, 椭圆或矩形中的每一个都称为树的节点.

该模型查看新示例(如上图的猫猫)并做出分类决策的方式是: 从树的最顶层节点(树的根节点)开始判断, 查看示例在该节点描述的特征是哪个值, 根据示例的特征值, 走向树的左边或右边.

树中最顶层的节点称为根节点.

椭圆形的节点(非顶层)称为决策节点. 决策节点查看特定的特征, 然后根据特征的值, 决定是向左还是向右.

位于底部矩形框的节点称为叶子节点.

一个训练集可能不止一个决策树. 有些会在训练集或交叉验证集或测试集上做得更好, 有些会做得更差.

决策树学习算法的工作是从所有可能的决策树中, 尝试选择一个希望在训练集上表现良好的树, 然后能理想地泛化到新数据.

构建

构建过程说明

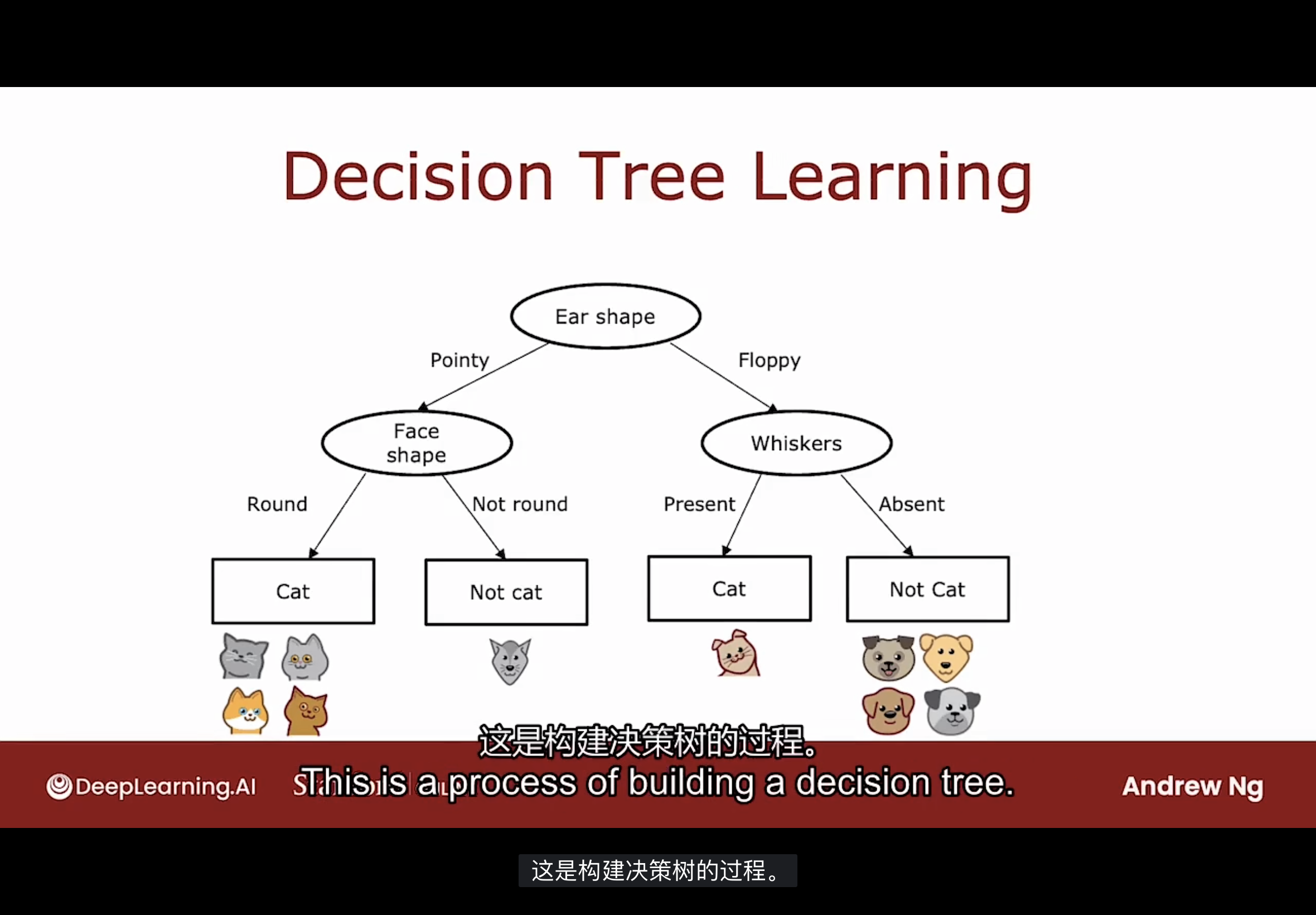
决策树学习模型构建的第一步是, 必须决定在根节点使用什么特征. 假定选择耳朵形状作为特征和根节点.

然后查看所有的训练示例, 根据根节点的特征, 按照耳朵形状的特征值将这些训练示例拆分. 假定选择5个尖耳朵的示例移到左边, 选择5个耳朵松软的示例移到右边.

第二步是只关注决策树的左侧部分(又称为左分支), 接下来使用什么样的特征来拆分左侧部分. 假设决定使用面部形状特征, 其中有4个圆脸形状的示例移动到左侧, 1个非圆脸的示例移动到右侧.

最后, 注意到左侧的4个示例都是猫, 右侧的示例不是猫, 因此没有进行下一步的分裂, 而是创建了两个个叶子节点, 一个是预测为猫的节点, 一个是预测不是猫的节点.

决策树的左侧分支完成此操作后, 继续在决策树的右侧分支重复类似的过程. 如图中所示, 根据胡须特征进行拆分.

构建过程中的决策

第一个关键决定

如何选择在每个决策节点上使用哪些特征进行拆分?

决策树将选择能把纯度最大化的拆分特征.

所谓纯度, 拆分能使尽可能接近全是分类标签为1和全是分类标签为0的子集. 比如如果能根据猫的DNA拆分, 两个数据子集都是完全纯的, 这意味着每个子集中只有一个类别.

现在的拆分特征有耳朵形状, 脸部形状, 是否有胡须(给定的数据就是这样的), 决策树学习算法必须在此特征之间进行选择: 哪个特征能使左右子分支上的标签纯度最高.

第二个关键决定

决定如何停止拆分?

1. 直到节点都是100%的一个分类, 如要么是猫, 要么不是.

2. 停止拆分, 不能让树超过最大深度. 树的深度是根节点到该特定节点的步数. 如果决定决策树的最大深度为2, 那么将不拆分低于此级别的任何节点, 防止树的深度大于2.

   限制决策树的原因是确保树不会变得太大和笨重; 通过保持树小, 不太容易过度拟合数据.

3. 使用优先级分数来决定停止拆分, 如果根据优先级分数拆分对纯度改进太小, 低于某个阈值, 此时拆分收益太小.

   使用优先级分数的原因也是确保树更小, 降低过度拟合.

4. 如果一个节点的示例数量低于某个阈值, 可能决定停止拆分.

   使用这种方式的原因也是让树更小并避免过度拟合.

纯度

熵

熵(Entropy)是衡量一组数据不纯程度的指标. 如下图所示

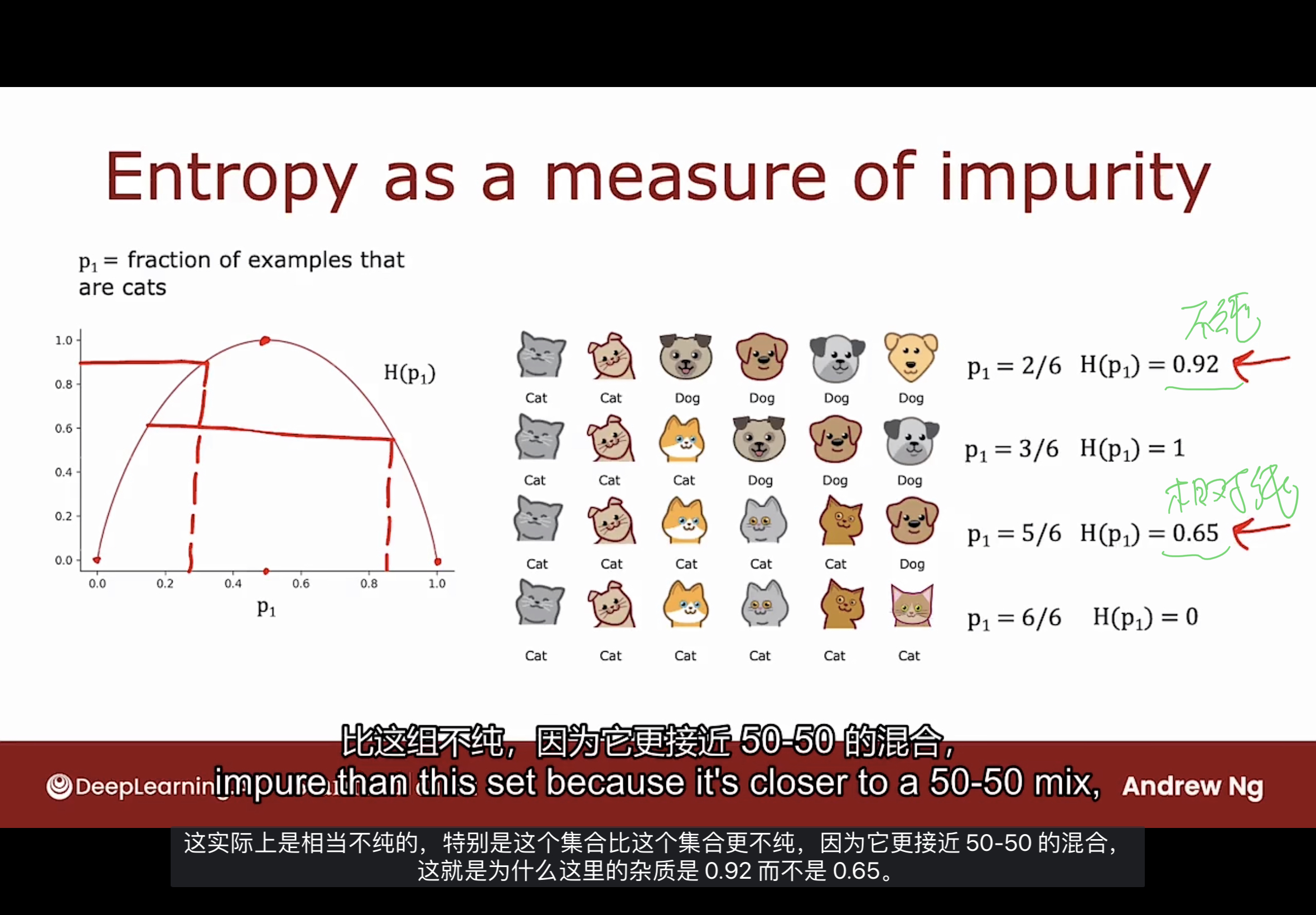
图中的p1代表的是数据集中是猫的比例. 坐标轴横轴是p1, 纵轴是熵值.

使用 $H(p_1)$ 来指代p1下的熵值. 可以看到$p_1 = 3 / 6$时熵值最大, 为1, 表明数据不纯程度较高.

计算 $H(p_1)$ 的公式, 注意对数是以2为底的.

$p_0 = 1 - p_1$

$H(p_1) = -p_1log_2(p1) - p_0log_2(p_0)$

将$p_0$代入可得:

$H(p_1) = -p_1log_2(p1) - (1-p_1)log_2(1-p_1)$

若有$p_0$或$p_1$为0, 则规定 $0log(0)=0$, 否则在技术上无定义, 实际上是负无穷大.

还有其他的熵函数, 比如Gini标准. 为简单起见, 本课程专注于使用通常适用于大多数应用程序的熵标准.

信息增益

Information Gain

在决策树中, 熵的减少称为信息增益.

计算信息增益, 从而选择在决策树的每个节点上使用哪些特征进行拆分. 如下图所示

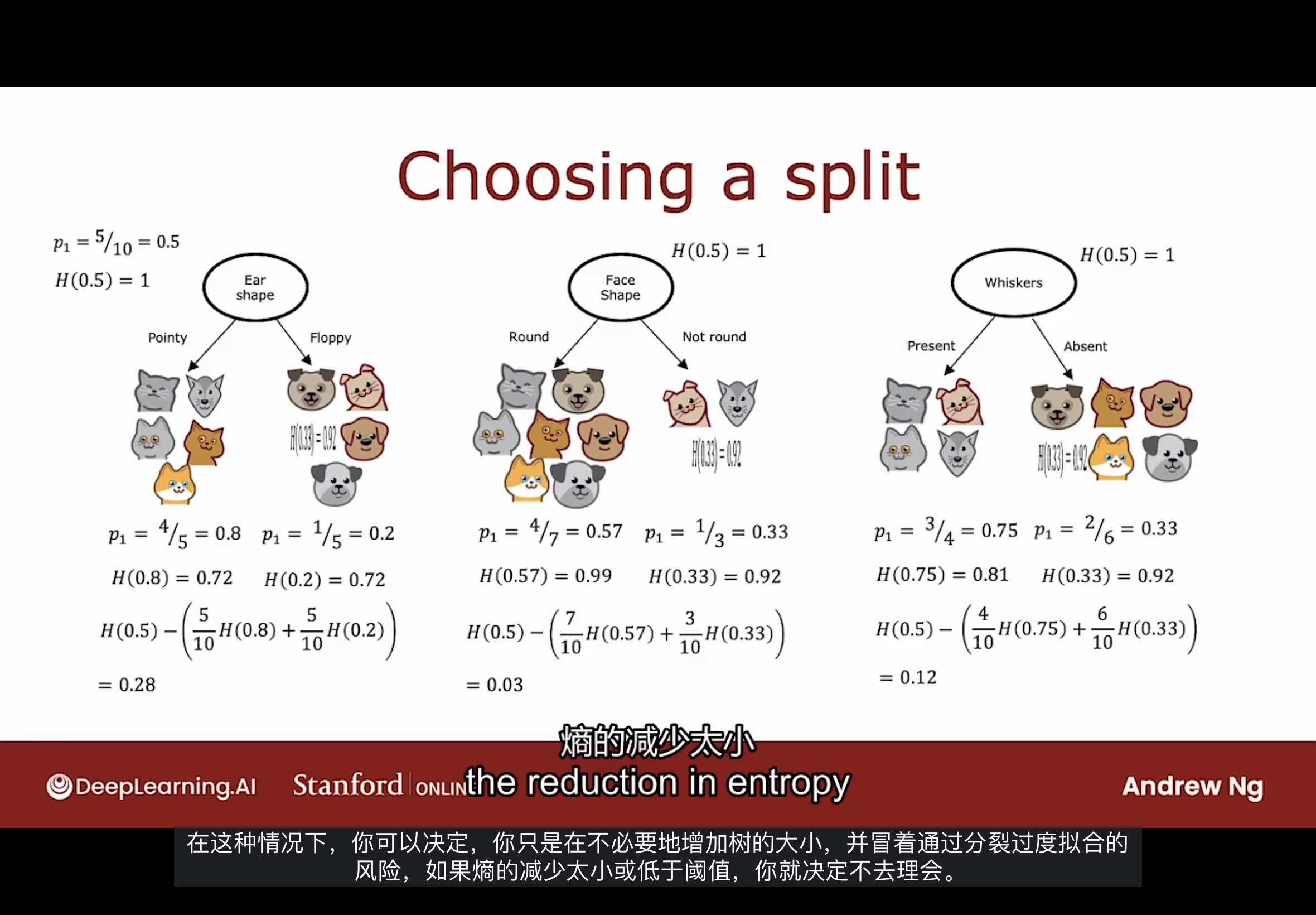
如果根据耳朵形状特征进行拆分, 得到左边的结果. 因左分支的五个动物里有四个是猫, 因此p1 = 4 / 5 = 0.8, 同样可计算右分支p2 = 1 / 5 = 0.2.

把计算熵的公式进行套用, 可得H(p1) = H(0.8) = 0.72, H(p2) = H(0.2) = 0.72

如果根据脸部形状特征进行拆分, 得到中间的结果. 如图所示

如果根据胡须特征进行拆分, 得到右边的结果. 如图所示

对这些计算出的熵值进行加权平均, 根据耳朵形状拆分的可得到:

$\frac{5}{10}H(0.8) + \frac{5}{10}H(0.2)$

注意加权的分数是左分支示例数量占总示例数量的比值.

选择拆分的方法是计算三个拆分特征中加权平均熵值最小的一个.

为何使用加权平均?

因为左或右子分支具有低熵更重要, 且取决于有多少示例进入左或右子分支.

如果左子分支有很多示例, 那么确保左子分支的熵值较低更为重要.

但在实践上, 将使用还未拆分时的熵值减去加权平均熵值的大小作为决策拆分特征的依据.

还未拆分时, 10个动物中有5个是猫, 因此p1 = 5 / 10 = 0.5, 于是H(0.5) = 1.

然后使用下面的公式, 以耳朵形状特征为例

$H(0.5) - (\frac{5}{10}H(0.8) + \frac{5}{10}H(0.2)) = 0.28$

得出的结果称为信息增益.

为何计算熵的减少而不是左右子分支的熵?

决定何时不再进行进一步拆分的停止标准之一就是熵的减少是否太小.

如果熵的减少很小时, 还进行拆分, 有着过度拟合的风险.

有上所述, 可得到信息增益的通用计算公式:

$H(p_1^{root}) - (w^{left}H(p_1^{left}) + w^{right}H(p_1^{right}))$

$H(p_1^{root})$是上一个节点或根节点的熵.

$w^{left}$, $w^{right}$ 分别是左子分支和右子分支占示例数量的比值(权重).

$H(p_1^{left})$, $H(p_1^{right})$ 分别是拆分后, 左右子分支的熵值.

结合熵的函数, 可以计算与选择任何相关特征关联的信息增益, 并进行拆分. 这将有希望提高在决策树的左右子分支上数据子集的纯度.

决策树构建过程

步骤如下:

1. 从树的根节点处的所有训练示例开始.

2. 计算所有可能特征的信息增益, 并选择要拆分的特征, 从而获得最高的信息增益.

3. 选择拆分特征后, 将数据集拆分为为两个子集, 并创建树的左右分支, 并根据子集的特征值把对应的训练示例发送到左侧或右侧分支.

4. 然后继续在树的左分支, 树的右分支上重复1到3的拆分过程, 直到:

   a.当一个节点上的数据集是100%一种类别时

   b.当分类节点导致超过设置的树的最大深度时

   c.当根据特征拆分后的信息增益小于阈值时

   d.当节点中示例数据的数量低于阈值时

5. 将继续重复拆分过程, 直到满足选择的停止条件(可能一个或多个)为止.

由上述描述, 可得知决策树的构建过程是一个递归过程.

同样理论上, 可使用交叉验证集来选择参数(如最大深度), 选取在交叉验证集上效果最好的参数.

One-Hot编码

到目前为止, 所见的示例中, 每个特征只能采用两个可能值中的一个, 如果超过两个特征值, 如何做呢? 使用one-hot编码. 如下图所示

现在耳朵形状不止有两个特征, 而是三个.

使用one-hot编码, 将采用三个可能值中的任何一个, 而不是使用耳朵形状的特征. 将创建三个特征, 第一个特征是动物是否有尖耳朵, 第二个特征是动物耳朵是否松软, 第三个特征是动物耳朵是否是椭圆形. 这三个特征的取值都是1和0.

通常, 如果一个分类特征取k个可能的值, 那么将通过创建k个只能取值0和1的二进制特征来替换该分类特征.

在所有的特征中, 每个示例在拆分的特征中, 恰好只有1个值等于1, 其中的一个特征将始终取值1, 即热特征, 故称为one-hot编码.

one-hot编码不仅能用于决策树模型, 同样也适用于训练神经网络. 如下图

可以看到其他的特征也都可以使用二进制数值进行代替, 因此该数据集能编码为5个特征的列表.

one-hot编码不仅适用于决策树模型, 也可以通过使用二进制数值1和0对分类特征进行编码, 这样数据集可以作为输入提供给神经网络.

那如果特征取值是连续的呢?

连续特征的拆分

如下图所示, 动物的体重是一个有连续值的特征, 那么如何拆分该特征呢?

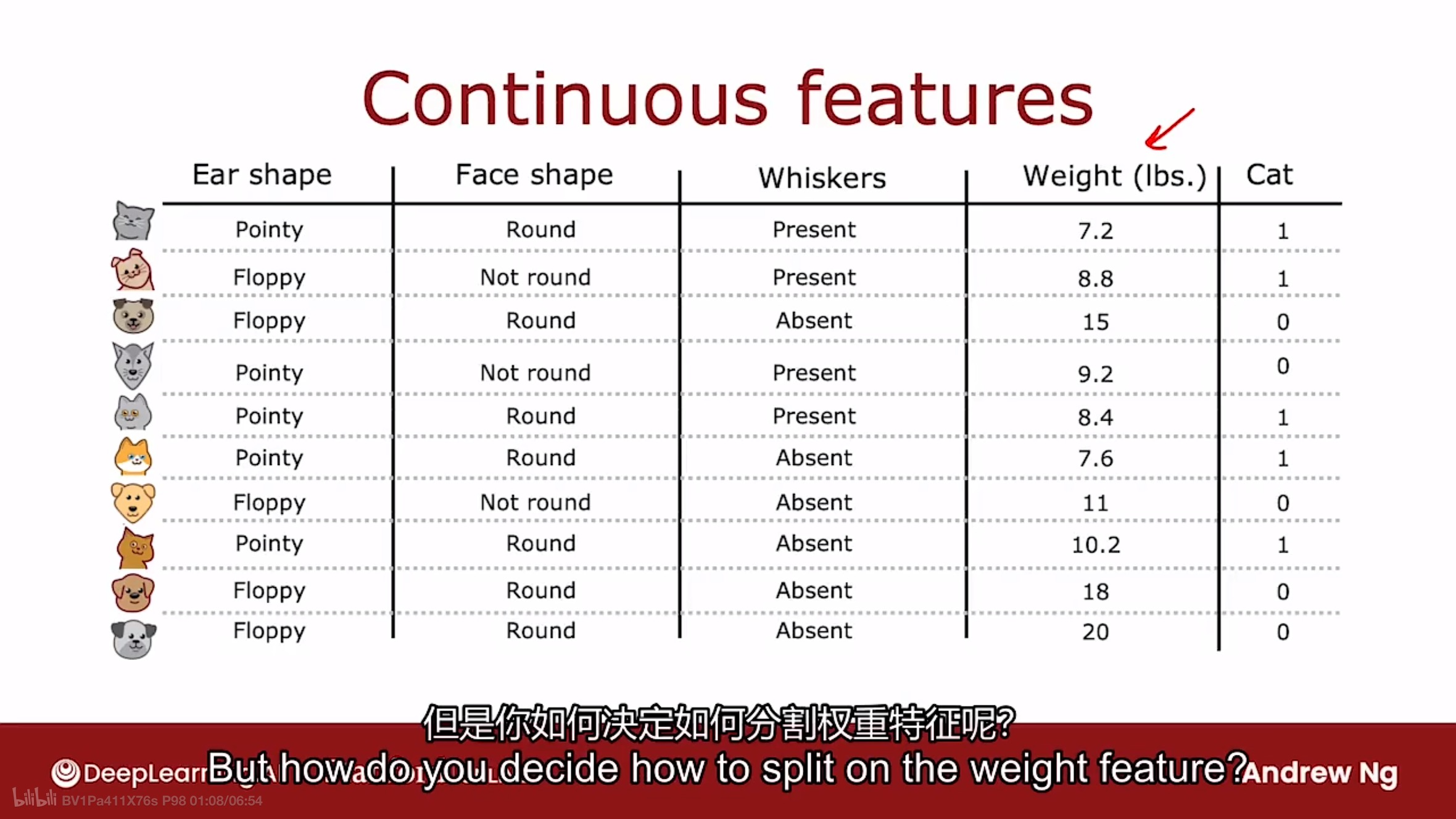
要根据体重特征十分小于或等于某个特征值来拆分数据.

对体重特征进行拆分时, 应该考虑通过选择特征值, 确保信息增益时最高的. 如下图

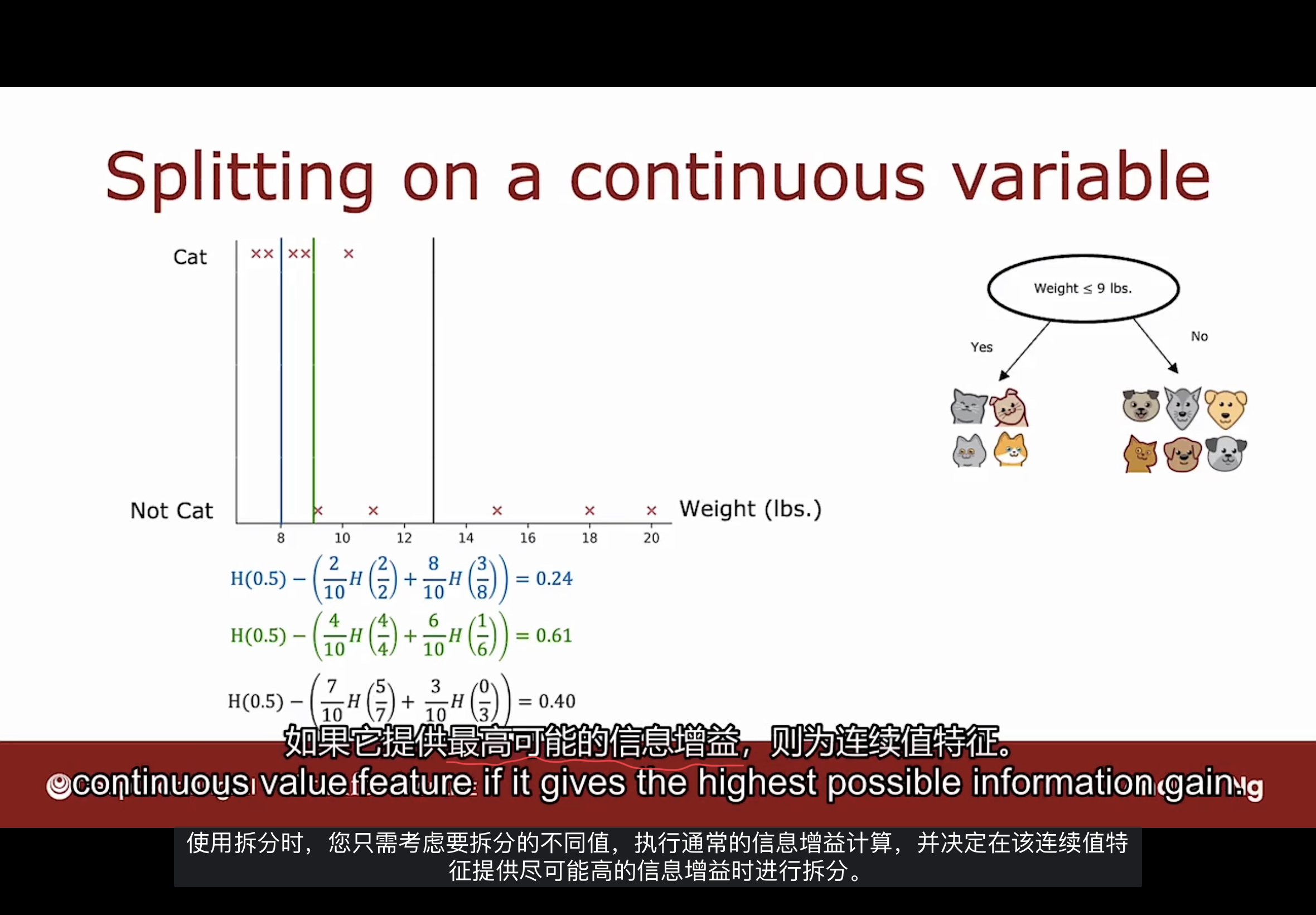
通过对体重阈值的选择, 使用计算信息增益的公式, 可得出当体重特征值为9时, 信息增益最佳.

通常的做法是根据此特征的值对所有示例数据进行排序, 并取所有处于已排序示例数据列表之间的所有中间的特征值. 通过计算信息增益这些特征值的信息增益, 来选择一个能提高最高信息增益的特征值. 然后选用此特征值作为特征拆分依据.

回归树

下图所示的例子是使用之前的三个特征, 预测动物的体重.

这是一个回归问题, 因为要预测一个体重数值. 如何用这样的数据集从头构建决策树以预测体重?

同样的, 先决定选择拆分哪个特征? 如下图, 根据三个特征分别拆分后的树

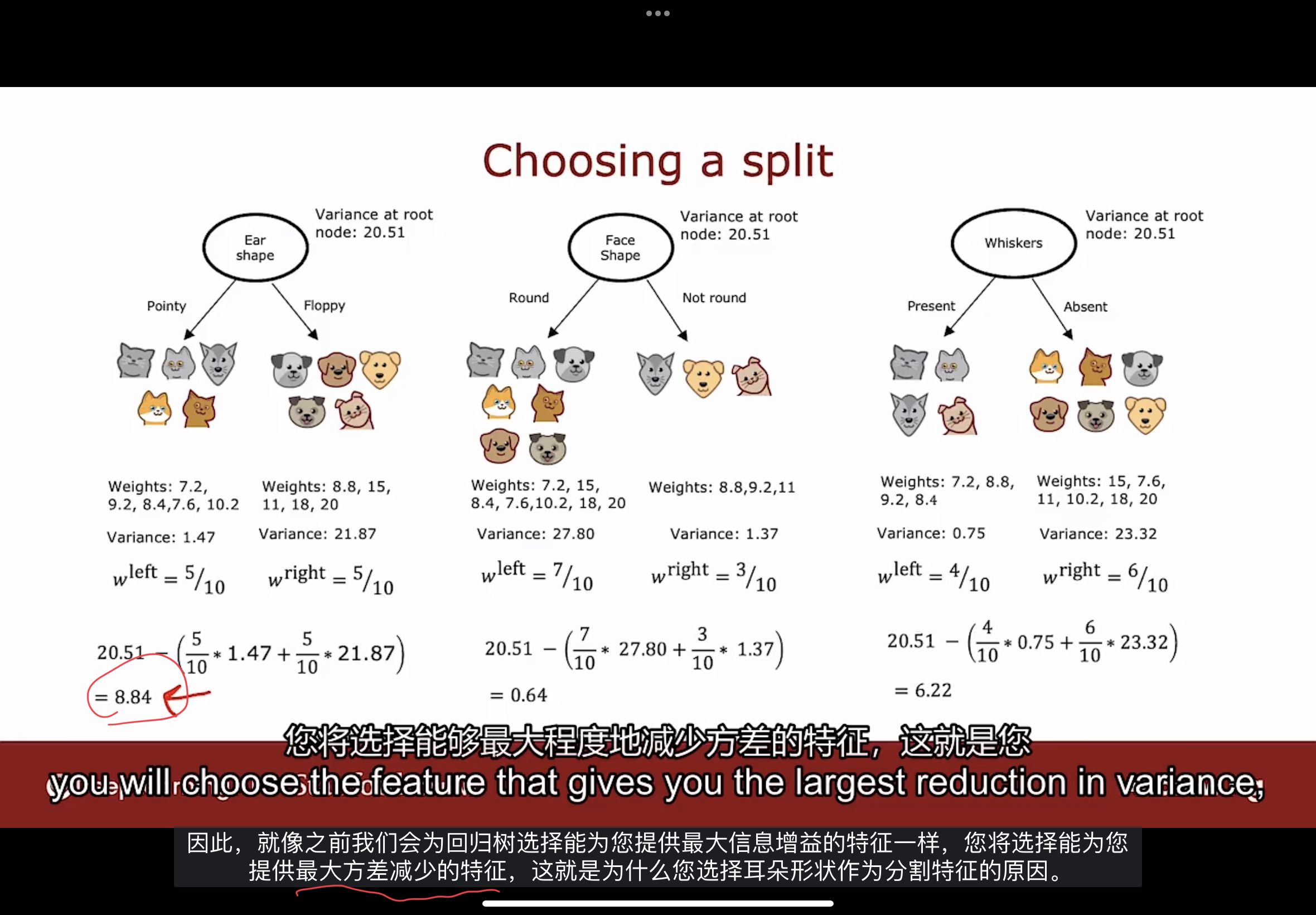
如何选择特征能更好的预测动物的体重呢?

在构建回归树时, 不是试图减少熵, 而是尝试减少每个数据子集值的权重方差.

需要使用到统计学的方差的概念. 以左边的回归树为例, 左分支的方差是1.47, 右分支的方差是21.87.

和决策树的熵计算方式一样, 计算加权平均方差值. 选择拆分特征的方法是选择最低的加权平均方差值.

和决策树的信息增益计算方式一样, 通过根节点的加权平均方差减去左右分支的加权平均方差的值, 选择能提供最大方差减少的特征.

如上图的计算表明, 使用耳朵形状作为特征能使方差减少最大化.

多个决策树

使用单个决策树的缺点之一是该决策树可能对数据中的微小变化高度敏感. 通过构建很多决策树, 能使学习算法更加健壮, 称之为树集成(Tree Ensemble).

下图是个树集成的例子

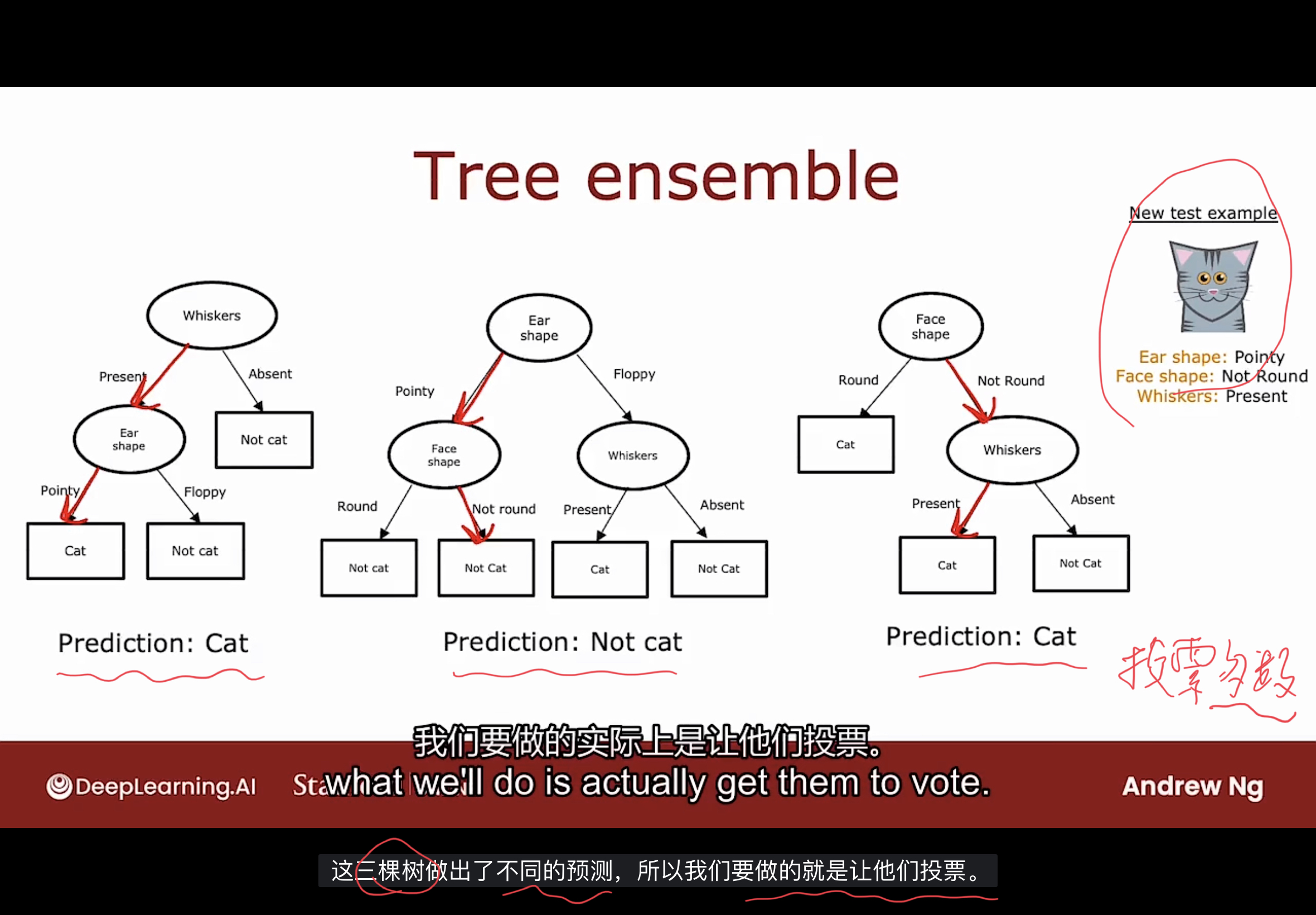
如果有三个决策树, 使用这些决策树分别对新示例上运行, 并让它们投票决定最终的预测结果.

使用树集成的原因是通过拥有大量决策树并让它们投票, 能使整体学习算法对任何一棵树可能正在做的事情不太敏感, 因为一个树只能获得其中一票, 这样能使整体学习算法更加健壮.

替换采样

使用替换采样(Sampling with Replacement)的技术来构建树集成.

假如有四个token, 分别是红黄绿蓝四种颜色, 通过放入一个集合中, 每次随机抽取(采样)一个token, 记录后放回原集合中(替换), 然后再次随机抽取, 直到完成4次随机抽取, 得到该集合的一个随机样本.

使用替换采样技术构建多个随机训练集的方式如下图

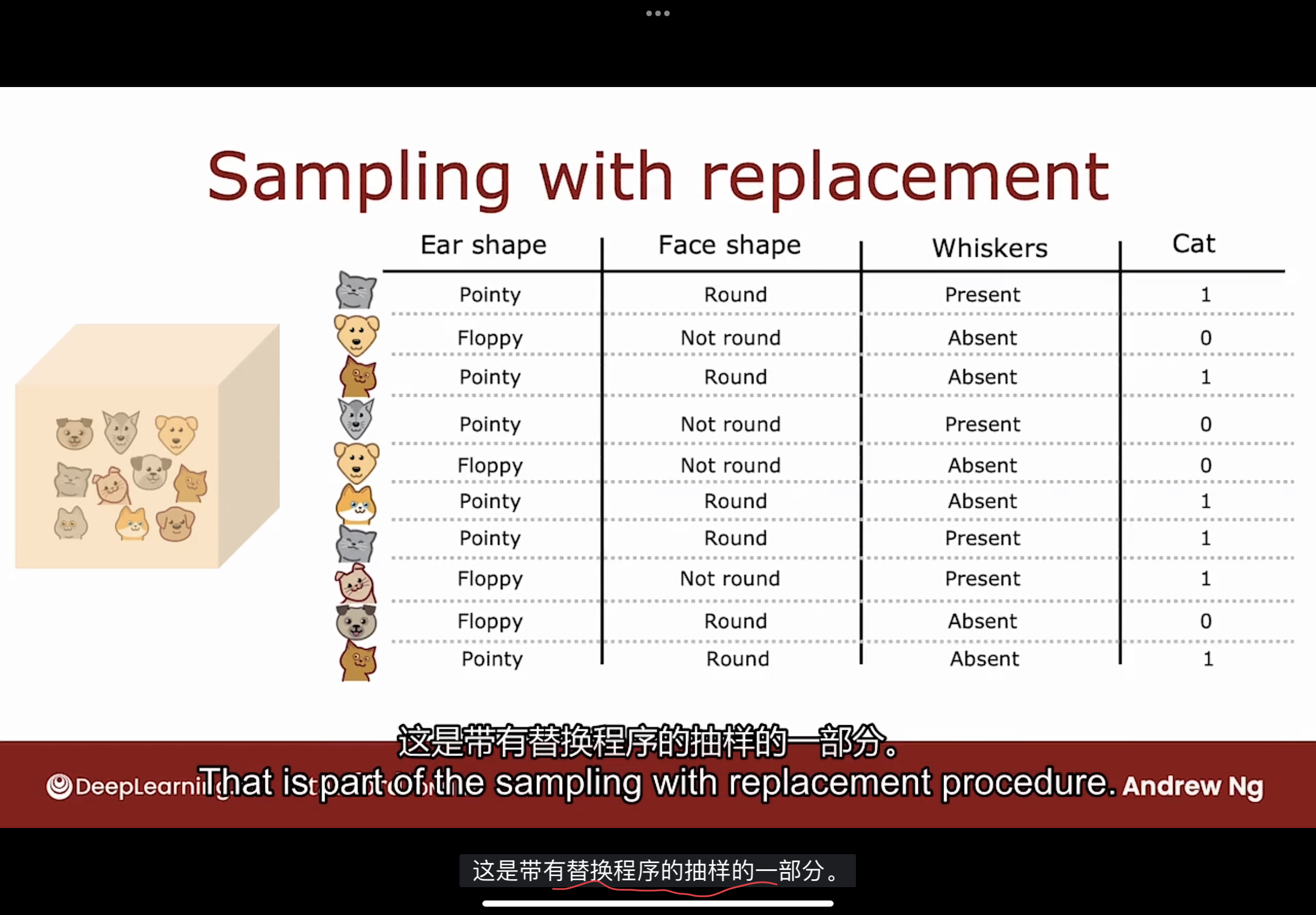
通过替换采样的方法, 可以得到上图所示的训练数据, 有些数据是重复的.

替换采样(有放回抽样)的过程可以构建一个新的训练集, 与原本的训练集有点相似, 但也有很大的不同, 这是构建树集成的关键.

随机森林算法

下图是生成树的集合的示例

给定一个大小为m的训练集, 循环1到B次, 每次循环使用替换采样生成大小也是m的新训练集, 然后在新训练集上构建决策树.

循环次数B的典型选择在100左右, 建议使用64, 128中的某个值. 将B值设置得更大不会损害性能, 当超过某个点后, 边际收益递减. 当远大于100时, 只会显著降低计算速度, 而不会显著提高整体算法的性能. 这种方式构建的树集成有时也称为袋装(bagged)决策树.

这种方式即使使用带有替换过程的采样, 有时最终还是在根节点上始终使用相同的或非常相似的拆分, 因此对算法做了一些修改, 以进一步尝试随机化选择每个特征. 如图

在每个节点上, 当选择要用于拆分的特征时, 如果有n个特征可用, 则选择k＜n个特征的随机特征子集, 并允许算法仅从该特征子集中进行选择.

即会选择k个特征作为允许的特征, 然后在k个特征中选择具有最高信息增益的特征作为使用拆分的特征选择.

当特征数量n很大时, 通常k值的典型选择是$k=\sqrt{n}$.

使用该随机森林的算法, 通常会比单个决策树更好地工作并更加强大.

原因是替换采样过程导致算法能探索数据的很多小变化, 并且通过训练不同的决策树, 对所有这些树平均了替换抽样程序导致的数据变化, 这意味着训练集的任何微小变化都不太可能对整个随机森林算法产生巨大的影响.

A joke

Where does a machine learning engineer go camping? In a random forest.

XGBoost算法

构建决策树和树集成的最常用方式是使用XGBoost算法. 该算法运行速度快, 代码开源, 易于使用, 且在很多机器学习比赛中获胜. 如下图

除了第一次循环构建决策树, 其余的循环次数中训练数据并不是相等的概率(1/m)被选中作为新的训练示例, 而是根据上次构建的决策树预测结果, 更有可能选择先前训练的分类错误或表现不佳的训练示例.

通过查看先前训练决策树中没有做得很好的地方, 然后在构建下一个决策树时, 将更多地关注尚未表现良好的示例, 而不是查看所有的训练示例, 下一个决策树尝试在尚未表现良好的示例子集中做得更好.

XGBoost(eXtreme Gradient Boosting)算法的优点:

1. 是提升树的开源实现
2. 非常快速高效
3. 很好的选择默认拆分标准和何时停止拆分的标准
4. 内置了正则化防止过度拟合
5. 在机器学习算法比赛中是一种竞争激烈的算法

XGBoost算法不使用替换采样, 实际上为不同的训练示例分配了不同的方法, 因此不需要生成许多随机选择的训练集, 比使用采样更有效.

使用XGBoost算法的代码

# 在分类Classification问题上使用
from xgboost import XGBClassifier
model = XGBClassifier()

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 在回归Regression问题上使用
from xgboost import XGBRegressor
model = XGBRegressor()

model.fit(X_train, y_train)
y_pred = model.predict(X_test)

何时使用决策树

决策树(树集成) VS 神经网络, 如下图

使用决策树

• 决策树(树集成)通常适用于表格或结构化数据
• 不建议在非结构化数据(图像, 音频, 视频, 文本等)上使用决策树和树集成
• 决策树和树集成的一个巨大优势是训练速度快, 能加快学习算法的构建训练诊断过程, 更有效地提升学习算法的性能.
• 小型决策树可能是人类可解释的, 当决集成比较大时, 且每棵树都有数百个节点, 然后弄清楚算法究竟在做什么确实变得困难, 可能需要一些单独的可视化技术.

推荐使用XGBoost算法构建决策树和树集成.

使用神经网络

• 神经网络适用于所有类型的数据, 包括结构化的和非结构化的
• 神经网络算法可能比决策树慢, 大型的神经网络需要很长时间来训练
• 能够和迁移学习一起使用, 这很重要, 因为对于很多应用程序, 只需一个小的数据集就可使用迁移学习.
• 如果构建一个由多个机器学习模型协同工作的系统, 那么多个神经网络串在一起并进行训练比多个决策树更容易. 大概原因是神经网络将输出y计算为平滑或连续函数, 并以此作为输入x, 可以使用梯度下降来训练它们. 但对于决策树, 一次就只能训练一颗决策树.

监督学习需要在训练集上带有标签, 而还有一组非常强大的算法称为无监督学习, 甚至不需要标签. 第三课见!

May the forest be with you.